题目内容
在△ABC中，动点P满足|
|2=|
|2-2
•
，则P点的轨迹一定通过△ABC的（ ）
| CA |
| CB |
| AB |
| CP |
| A、外心 | B、内心 | C、重心 | D、垂心 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：先将题设中的等式移项，利用|
|2=
2、|
|2=
2及平方差公式化简，再利用两向量垂直的充要条件得到线段的位置关系，从而获得动点P的轨迹．
| CA |
| CA |
| CB |
| CB |
解答：
解：由|
|2=|
|2-2
•
，
得|
|2-|
|2=2
•
，即
2-
2=2
•
，
从而（
+
）•（
-
）=2
•
，
∴（
+
）•
=2
•
，
∴
•(
+
-2
)=0，
∵P为动点，∴
+
-2
≠
，
∴
⊥(
+
-2
)，
设M是AB中点，则
⊥(2
-2
)，
∴
⊥
，
∴P在AB的垂直平分线上，
∴P点轨迹一定通过△ABC的外心．
故选A．
| CA |
| CB |
| AB |
| CP |
得|
| CB |
| CA |
| AB |
| CP |
| CB |
| CA |
| AB |
| CP |
从而（
| CB |
| CA |
| CB |
| CA |
| AB |
| CP |
∴（
| CB |
| CA |
| AB |
| AB |
| CP |
∴
| AB |
| CB |
| CA |
| CP |
∵P为动点，∴
| CB |
| CA |
| CP |
| 0 |
∴
| AB |
| CB |
| CA |
| CP |
设M是AB中点，则
| AB |
| CM |
| CP |
∴
| AB |
| PM |
∴P在AB的垂直平分线上，
∴P点轨迹一定通过△ABC的外心．
故选A．
点评：1．从求解过程可以看出，对于给出向量式，求解动点轨迹问题，一般是先将向量式化为最简，再根据几何图形的特征探究动点，定点和各线段之间的联系．应注意两点：
（1）应熟练向量的加、减法运算（尤其是三角形法则，平行四边形法则），数乘运算，数量积的运算及性质．
（2）充分利用已知中提供的图形信息，如线段长度相等，直角三角形，中点等，必要时可添加适当的辅助线或点．
2．应熟练掌握三角形各“心”的含义及性质，如外心是三角形外接圆的圆心，即三边垂直平分线的交点；内心是三角形内切圆的圆心，即三内角平分线的交点；重心是三边中线的交点；垂心是三高线所在直线的交点．
（1）应熟练向量的加、减法运算（尤其是三角形法则，平行四边形法则），数乘运算，数量积的运算及性质．
（2）充分利用已知中提供的图形信息，如线段长度相等，直角三角形，中点等，必要时可添加适当的辅助线或点．
2．应熟练掌握三角形各“心”的含义及性质，如外心是三角形外接圆的圆心，即三边垂直平分线的交点；内心是三角形内切圆的圆心，即三内角平分线的交点；重心是三边中线的交点；垂心是三高线所在直线的交点．
练习册系列答案
相关题目
如图，在正方体ABCD-A1B1C1D1中，E、F分别是棱BC、C1D1的中点，则EF与平面BB1D1D的位置关系是已知f（n+1）=
，f（1）=1，（n∈N*），猜想f（n）的表达式为（ ）
| 2f(n) |
| f(n)+2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若二面角M-l-N的平面角大小为
π，直线m⊥平面M，则平面N内的直线与m所成角的取值范围是（ ）
| 2 |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[0，
|
设F1、F2分别是双曲线
-
=1（a＞0，b＞0）的左、右焦点，如双曲线上存在点P，使得∠PF1F2=30°，∠PF2F1=120°，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=ax-
的图象可能是（ ）
| 1 |
| a |
A、 |
B、 |
C、 |
D、 |
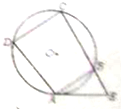如图，四边形ABCD内接于圆O，点E在CB的延长线上，AE切圆于O于点A，若AB∥CD，AD=4| 3 |
| 3 |
| A、36 | ||
| B、6 | ||
| C、24 | ||
D、2
|