设变量x.y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$.则z=x-4y的最小值为-6．题目和参考答案——青夏教育精英家教网—

题目内容

11．设变量x，y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$，则z=x-4y的最小值为-6．

分析由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．

解答解：画出不等式组表示的平面区域，

由图可知，当直线z=x-4y过点A，C时z分别取得最大值和最小值．
又A（1，0），B（0，1），C（2，2），
∴z_min=2-4×2=-6．
故答案为：-6．

点评本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

2．a、b为非零实数，且a＜b，则下列命题成立的是（　　）

A．

a²＜b²

B．

$\frac{1}{{a{b^2}}}$＜$\frac{1}{{{a^2}b}}$

C．

a²b＜ab²

D．

$\frac{b}{a}$＜$\frac{a}{b}$

19．

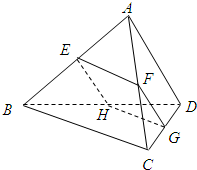如图，空间四边形ABCD的对棱AD、BC成90°的角，且AD=BC=a，平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H．E在AB上，截面EGFH的最大面积是$\frac{1}{4}{a}^{2}$．

6．计算：${∫}_{-2}^{2}（{x}^{3}+\sqrt{4-{x}^{2}}）dx$=2π．

16．已知${f_0}（x）=x{e^x}，{f_1}（x）={f'_0}（x），{f_2}（x）={f'_1}（x），…，{f_n}（x）={f'_{n-1}}（x）（n∈{N^+}）$．
（Ⅰ）请写出f_n（x）的表达式（不需证明）；
（Ⅱ）设f_n（x）的极小值点为P_n（x_n，y_n），求y_n；
（Ⅲ）设${g_n}（x）=-{x^2}-2（n+1）x-8n+8$，g_n（x）的最大值为a，f_n（x）的最小值为b，求b-a的最小值．

3．对任意实数x，若不等式x+|3x-2a|≥3恒成立，则实数a的取值范围是[$\frac{9}{2}$，+∞）．

20．方程组$\left\{\begin{array}{l}3x+5y+6=0\\ 4x-3y-7=0\end{array}\right.$的增广矩阵是$[\begin{array}{l}{3}&{5}&{-6}\\{4}&{-3}&{7}\end{array}]$．

1．像“3，4，5”这样能够成直角三角形的数称为勾股数，又称为（　　）

试题分类