Question

已知圆P：x²+y²=4y及抛物线S：x²=8y，过圆心P作直线l，此直线与上述两曲线的四个交点，自左向右顺次记为A，B，C，D，如果线段AB，BC，CD的长按此顺序构成一个等差数列，则直线l的斜率为（　　）

• A、±

  2

  2

• B、

  2

  2

• C、±

  2

• D、

  2

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：先确定圆P的标准方程，求出圆心与直径长，设出l的方程，代入抛物线方程，求出|AD|，利用线段AB、BC、CD的长按此顺序构成一个等差数列，可得|AD|=3|BC|，求出k的值，可得直线l的斜率的值．

解答： 解：圆P的方程为x²+（y-2）²=4，则其直径长|BC|=4，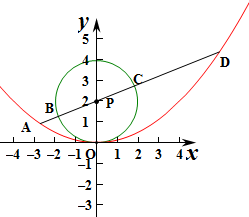
圆心为P（0，2），
∵AB，BC，CD的长按此顺序构成一个等差数列，
∴|AB|+|CD|=2|BC|=8，
即|AD|=|AB|+|BC|+|CD|=3|BC|=12，
设直线l的方程为y=kx+2，代入抛物线方程x²=8y得：x²-8kx-16=0，
设A（x₁，y₁），D（x₂，y₂），
有

△=64k2+64＞0 x1+x2=8k x1x2=-16

，
∴|AD|=

(1+k2)[(x1+x2)2-4x1x2]

(1+k2)(64k2+64)

=8（k²+1），
∴8（k²+1）=12，
即k²=

1

2

，
解得k=±

2

2

，
∴直线l的斜率为±

2

2

，
故选：A．

点评：本题考查直线与圆、抛物线的位置关系，考查等差数列，考查学生的计算能力，确定|AD|是关键，综合性较强，运算量较大．