题目内容
以下命题:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程
=
x+
恒过样本中心(
,
),且至少过一个样本点;
③复数z=(a-2i)i(a∈R,i为虚数单位)在复平面内对应的点为M,则“a<0“是“点M在第四象限”的充要条件.
其中真命题的个数为( )
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
③复数z=(a-2i)i(a∈R,i为虚数单位)在复平面内对应的点为M,则“a<0“是“点M在第四象限”的充要条件.
其中真命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:由系统抽样间隔号的求法求出间隔号判断①;
利用线性回归直线方程的意义,即恒过样本中心点但不一定过样本点判断②;
由充要条件的概念判断③.
利用线性回归直线方程的意义,即恒过样本中心点但不一定过样本点判断②;
由充要条件的概念判断③.
解答:
解:对于①,总体容量N=800,样本容量n=40,则用系统抽样的分段的间隔k=
=20,命题①为假命题;
对于②,线性回归直线方程
=
x+
恒过样本中心(
,
),但不一定过样本点,命题②为假命题;
对于③,∵复数z=(a-2i)在复平面内对应的点M(a,-2),
对于④,∵复数z=(a-2i)i=2+ai(a∈R,i为虚数单位)在复平面内对应的点为M,则“a<0“是“点M在第四象限”的充要条件.命题③为真命题.
∴真命题的个数为1.
故选:B.
| 800 |
| 40 |
对于②,线性回归直线方程
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
对于③,∵复数z=(a-2i)在复平面内对应的点M(a,-2),
对于④,∵复数z=(a-2i)i=2+ai(a∈R,i为虚数单位)在复平面内对应的点为M,则“a<0“是“点M在第四象限”的充要条件.命题③为真命题.
∴真命题的个数为1.
故选:B.
点评:本题考查了命题的真假判断与应用,关键是对教材基础概念和基础知识的熟练掌握,是中档题.

练习册系列答案
相关题目
已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线l,此直线与上述两曲线的四个交点,自左向右顺次记为A,B,C,D,如果线段AB,BC,CD的长按此顺序构成一个等差数列,则直线l的斜率为( )
A、±
| ||||
B、
| ||||
C、±
| ||||
D、
|
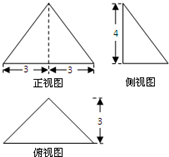 如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为( )
如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=sinx在区间(0,5π)上可找到n(n≥2)个不同数x1,x2,…,xn,使得:
=
=…=
,则自然数n的所有可能取值集合为( )
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(xn) |
| xn |
| A、{2,3} |
| B、{2,3,4} |
| C、{2,3,4,5} |
| D、{3,4,5,6} |
已知2x=3y=a,且
+
=2,则a的值为( )
| 1 |
| x |
| 1 |
| y |
A、
| ||
| B、6 | ||
C、±
| ||
| D、36 |