题目内容
9.已知a,b,c分别是△ABC的内角A,B,C的对边,且c=2,C=$\frac{π}{3}$.(Ⅰ)若△ABC的面积等于$\sqrt{3}$,求a,b;
(Ⅱ)若sinC+sin(B-A)=2sin2A,求锐角A的值.
分析 本题考查正弦定理,余弦定理以及任意三角形的面积公式
(Ⅰ)直接由余弦定理,任意三角形的面积公式,求出a,b.
(Ⅱ)利用三角形的内角和为π,可以消去C,从而利用两角和与差的公式即可解出A的值.
解答 解:(Ⅰ)∵c=2,C=$\frac{π}{3}$.由任意三角形的面积公式S=$\frac{1}{2}$absinc,
可得:ad=4
又由余弦定理:$4={a}^{2}+{b}^{2}-2abcos\frac{π}{3}={a}^{2}+{b}^{2}-ab$
联立$\left\{\begin{array}{l}{ab=4}\\{{a}^{2}+{b}^{2}-ab=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$
∴a=2,b=2
(Ⅱ)∵sinC+sin(B-A)=2sin2A,A+B+C=π,
∴sin(π-A-B)+sin(B-A)=2sin2A
?sin(A+B)+sin(B-A)=2sinAcosA
?sinBcosA=2sinAcosA.
∵cosA≠0,
∴sinB=2sinA.
由正弦定理,可得:b=2a.
由余弦定理:$4={a}^{2}+{b}^{2}-2abcos\frac{π}{3}={a}^{2}+{b}^{2}-ab$
联立$\left\{\begin{array}{l}{b=2a}\\{{b}^{2}+{a}^{2}-ab=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{2\sqrt{3}}{3}}\\{b=\frac{4\sqrt{3}}{3}}\end{array}\right.$
由正弦定理:$\frac{a}{sinA}=\frac{c}{sinC}$
∴sinA=$\frac{1}{2}$
又∵A是锐角.
∴A=$\frac{π}{6}$
点评 本题考查正弦定理,余弦定理以及任意三角形的面积公式,对公式的灵活运用及计算能力,属于基础题.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-3,3] | C. | [-$\sqrt{3}$,3] | D. | [-3,$\sqrt{3}$] |
| A. | 540 | B. | 240 | C. | 180 | D. | 150 |
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | $\frac{{\sqrt{2}-1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{3}$ |
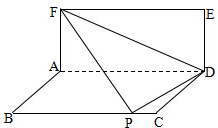 已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.
已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.