题目内容
4.已知A(3,$\sqrt{3}$),O是坐标原点,点P(x,y)的坐标满足$\left\{\begin{array}{l}{\sqrt{3}-y≤0}\\{x-\sqrt{3}+0≥0}\\{y≥0}\end{array}\right.$,设Z为$\overrightarrow{OA}$在$\overrightarrow{OP}$上的投影,则Z的取值范围是( )| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-3,3] | C. | [-$\sqrt{3}$,3] | D. | [-3,$\sqrt{3}$] |
分析 作出不等式组对应的平面区域,利用向量投影的定义计算z的表达式,利用数形结合即可得到结论.
解答 解:设z表示向量$\overrightarrow{OA}$在$\overrightarrow{OP}$方向上的投影,
∴z=$\frac{\overrightarrow{OP}•\overrightarrow{OA}}{|\overrightarrow{OA}|}$=$\frac{3x+\sqrt{3}y}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$x+$\frac{1}{2}$y,
即y=-$\sqrt{3}$x+2z,
作出不等式组对应的平面区域如图:
平移直线y=-$\sqrt{3}$x+2z,当y=-$\sqrt{3}$x+2z经过点B时直线y=-$\sqrt{3}$x+2z的截距最大,此时z最大,
当y=-$\sqrt{3}$x+2z经过点C(-2,0)时,直线的截距最小,此时z最小.此时zmin=$\sqrt{3}$,
由$\left\{\begin{array}{l}{\sqrt{3}x-y=0}\\{x-\sqrt{3}y+2=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=1}\\{y=\sqrt{3}}\end{array}\right.$,即B(1,$\sqrt{3}$),
此时最大值z=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故z的取值范围是[-$\sqrt{3}$,$\sqrt{3}$],
故选:B.
点评 本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
15.在平面直角坐标系中,过(1,0)点且倾率为-1的直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.青岛发生输油管道爆炸事故造成胶州湾局部污染,国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干组成研究小组赴泄油海域工作,有关数据见表一(单位:人)
表一:
表二:
海洋生物专家为了检测该地污染后对海洋生物身体健康的影响,随机选取了110只海豚进行了检测,并将有关数据整理为不完整的2×2的列联表,如表二.
(1)求研究小组的人数;
(2)写出表二中A,B,C,D,E的值,并做出判断能否有99%的把握认为“海豚身体健康与受到污染有关”;(3)若从环保小组的环保专家和油气专家随机选2人撰写研究报告,求其中恰好有1人为环保专家的概率.
解答时可参考下面公式及临界值表:k0=$\frac{n(ad-bc)^{2}}{(a+b)(b+d)(a+b)(c+b)}$.
表一:
| 相关人员数 | 抽取人数 | |
| 环保专家 | 24 | x |
| 海洋生物专家 | 48 | 4 |
| 油气专家 | 36 | y |
| 重度污染 | 轻度污染 | 合计 | |
| 身体健康 | 30 | A | 50 |
| 身体不健康 | B | 10 | 60 |
| 合计 | C | D | E |
(1)求研究小组的人数;
(2)写出表二中A,B,C,D,E的值,并做出判断能否有99%的把握认为“海豚身体健康与受到污染有关”;(3)若从环保小组的环保专家和油气专家随机选2人撰写研究报告,求其中恰好有1人为环保专家的概率.
解答时可参考下面公式及临界值表:k0=$\frac{n(ad-bc)^{2}}{(a+b)(b+d)(a+b)(c+b)}$.
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 0.635 | 7.879 |
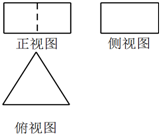 如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.
如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.