题目内容
已知向量
,
,
满足:
+2
+3
=
,则S△ABC:S△OBC=( )
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| 0 |
| A、12 | B、6 | C、3 | D、2 |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:设直线AO与直线BC的交点为点M,则△OBC和△ABC面积比为|OM|:|AM|,平面向量基本定理,结合向量的运算,寻找
,
的线性关系,从而求出两三角形的面积比.
| AM |
| OM |
解答:
解:如图,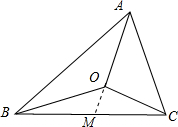 ;
;
设直线AO与直线BC的交点为点M,则
△OBC和△ABC面积比为|OM|:|AM|;
设
=x
,
∵
+2
+3
=
,∴
=x(-2
-3
)=-2x
-3x
;
由平面向量的基本定理得,-2x-3x=1,
解得x=-
;所以
=6
∴△OBC和△ABC的面积比为
|OM|:|AM|=1:6;
故选:B
 ;
;设直线AO与直线BC的交点为点M,则
△OBC和△ABC面积比为|OM|:|AM|;
设
| OM |
| OA |
∵
| OA |
| OB |
| OC |
| 0 |
| OM |
| OB |
| OC |
| OB |
| OC |
由平面向量的基本定理得,-2x-3x=1,
解得x=-
| 1 |
| 5 |
| AM |
| OM |
∴△OBC和△ABC的面积比为
|OM|:|AM|=1:6;
故选:B
点评:本题考查了平面向量的基本定理的应用问题,解题时应按照平面向量的运算法则进行解答..

练习册系列答案
相关题目
下列函数是幂函数的是( )
| A、y=2x2 | ||
| B、y=x3+x | ||
C、y=x
| ||
| D、y=3x |
已知函数f(x)=
若关于x 的方程f(x)=kx有两个不同的实根,则数k的取值范围是( )
|
| A、(0,1) |
| B、[0,2] |
| C、(0,1] |
| D、(0,2] |
若关于x的方程x2+ax+a2-1=0有一个正根和一个负根,则实数a的取值范围为( )
A、-
| ||||||||
B、-
| ||||||||
| C、-1≤a≤1 | ||||||||
| D、-1<a<1 |
函数f(x)=
的单调递减区间是( )
| lnx |
| x |
| A、[e,+∞) |
| B、[1,+∞) |
| C、(0,e] |
| D、(0,1) |
三边长分别为4,5,6的三角形的形状是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上答案均有可能 |
函数y=sinx是( )
| A、最小正周期为2π的偶函数 |
| B、最小正周期为π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为π的奇函数 |