题目内容
设函数f(x)=lnx-ax,
(Ⅰ)当a>0时,求函数f(x)在区间[1,e]内的最大值;
(Ⅱ)当a=-1时,方程2mf(x)=x2有唯一实数解,求正数m的值.
(Ⅰ)当a>0时,求函数f(x)在区间[1,e]内的最大值;
(Ⅱ)当a=-1时,方程2mf(x)=x2有唯一实数解,求正数m的值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)对a分类讨论,利用导数的运算法则研究函数的单调性即可得出;
(2)方程2mf(x)=x2有唯一实数解,即x2-2mlnx-2mx=0有唯一实数解,设g(x)=x2-2mlnx-2mx,利用导数可得其最小值为g(x2).
则
,即2lnx2+x2-1=0.设h(x)=2lnx+x-1(x>0),再利用导数研究其单调性即可得出.④
(2)方程2mf(x)=x2有唯一实数解,即x2-2mlnx-2mx=0有唯一实数解,设g(x)=x2-2mlnx-2mx,利用导数可得其最小值为g(x2).
则
|
解答:
解:(1)f′(x)=
-a=
, x>0.
令f'(x)=0得x=
.
∵x∈(0,
)时,f'(x)>0,x∈(
,+∞)时,f'(x)<0,
∴f(x)在(0,
)递增,在(
,+∞)递减.
①当0<
≤1即a≥1时,f(x)在[1,e]上递减,
∴x=1时f(x)取最大值f(1)=-a.
②当1<
<e即
<a<1时,f(x)在(1,
)递增,在(
,e)递减,
∴x=
时,f(x)取最大值f(
)=-lna-1.
③当
≥e即0<a≤
时,f(x)在(1,e)递增,
∴x=e时f(x)取最大值f(e)=1-ae.
(2)∵方程2mf(x)=x2有唯一实数解,即x2-2mlnx-2mx=0有唯一实数解,
设g(x)=x2-2mlnx-2mx,则g′(x)=
.
令g'(x)=0,x2-mx-m=0.
∵m>0,x>0,
∴x1=
<0(舍去),x2=
.
当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)上单调递减;当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)上单调递增.
∴g(x)最小值为g(x2).
则
,即
∴2mlnx2+mx2-m=0即2lnx2+x2-1=0.
设h(x)=2lnx+x-1(x>0),h′(x)=
+1>0恒成立,
故h(x)在(0,+∞)单调递增,h(x)=0至多有一解.
又h(1)=0,∴x2=1,即
=1,解得m=
.
| 1 |
| x |
| 1-ax |
| x |
令f'(x)=0得x=
| 1 |
| a |
∵x∈(0,
| 1 |
| a |
| 1 |
| a |
∴f(x)在(0,
| 1 |
| a |
| 1 |
| a |
①当0<
| 1 |
| a |
∴x=1时f(x)取最大值f(1)=-a.
②当1<
| 1 |
| a |
| 1 |
| e |
| 1 |
| a |
| 1 |
| a |
∴x=
| 1 |
| a |
| 1 |
| a |
③当
| 1 |
| a |
| 1 |
| e |
∴x=e时f(x)取最大值f(e)=1-ae.
(2)∵方程2mf(x)=x2有唯一实数解,即x2-2mlnx-2mx=0有唯一实数解,
设g(x)=x2-2mlnx-2mx,则g′(x)=
| 2x2-2mx-2m |
| x |
令g'(x)=0,x2-mx-m=0.
∵m>0,x>0,
∴x1=
m-
| ||
| 2 |
m+
| ||
| 2 |
当x∈(0,x2)时,g'(x)<0,g(x)在(0,x2)上单调递减;当x∈(x2,+∞)时,g'(x)>0,g(x)在(x2,+∞)上单调递增.
∴g(x)最小值为g(x2).
则
|
|
∴2mlnx2+mx2-m=0即2lnx2+x2-1=0.
设h(x)=2lnx+x-1(x>0),h′(x)=
| 2 |
| x |
故h(x)在(0,+∞)单调递增,h(x)=0至多有一解.
又h(1)=0,∴x2=1,即
m+
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了问题的转化能力,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
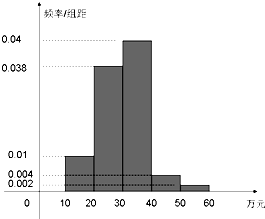 在某市的人大贿选案中,经调查统计该市人大代表的受贿情况的频率分布直方图如图:其中受贿[10,20]万元的有10人.
在某市的人大贿选案中,经调查统计该市人大代表的受贿情况的频率分布直方图如图:其中受贿[10,20]万元的有10人.