题目内容
已知函数f(x)=
,a∈R.
(1)若函数y=f(x)在x=1处取得极值,求a的值;
(2)若函数y=f(x)的图象上存在两点关于原点对称,求a的范围.
|
(1)若函数y=f(x)在x=1处取得极值,求a的值;
(2)若函数y=f(x)的图象上存在两点关于原点对称,求a的范围.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)当x>0时,f'(x)=2(ex-x+a)从而f'(1)=0,解出即可,(2)由题意得到方程组,求出a的表达式,设h(x)=
(x>0),再通过求导求出函数h(x)的最小值,问题得以解决.
| 2ex |
| x |
解答:
解:(1)当x>0时,
f(x)=2ex-(x-a)2+3,
f′(x)=2(ex-x+a),
∵y=f(x)在x=1处取得极值,
∴f′(1)=0,即2(e-1+a)=0
解得:a=1-e,经验证满足题意,
∴a=1-e.
(2)y=f(x)的图象上存在两点关于原点对称,
即存在y=2ex-(x-a)2+3图象上一点(x0,y0)(x0>0),
使得(-x0,-y0)在y=x2+3ax+a2-3的图象上
则有
,
∴2ex0-(x0-a)2+3=-x02+3ax0-a 2+3
化简得:a=
,即关于x0的方程在(0,+∞)内有解
设h(x)=
(x>0),则h′(x)=
∵x>0
∴当x>1时,h'(x)>0;当0<x<1时,h'(x)<0
即h(x)在(0,1)上为减函数,在(1,+∞)上为增函数
∴h(x)≥h(1)=2e,且x→+∞时,h(x)→+∞;x→0时,h(x)→+∞
即h(x)值域为[2e,+∞),
∴a≥2e时,方程a=
在(0,+∞)内有解
∴a≥2e时,y=f(x)的图象上存在两点关于原点对称.
f(x)=2ex-(x-a)2+3,
f′(x)=2(ex-x+a),
∵y=f(x)在x=1处取得极值,
∴f′(1)=0,即2(e-1+a)=0
解得:a=1-e,经验证满足题意,
∴a=1-e.
(2)y=f(x)的图象上存在两点关于原点对称,
即存在y=2ex-(x-a)2+3图象上一点(x0,y0)(x0>0),
使得(-x0,-y0)在y=x2+3ax+a2-3的图象上
则有
|
∴2ex0-(x0-a)2+3=-x02+3ax0-a 2+3
化简得:a=
| 2ex0 |
| x0 |
设h(x)=
| 2ex |
| x |
| 2ex(x-1) |
| x2 |
∵x>0
∴当x>1时,h'(x)>0;当0<x<1时,h'(x)<0
即h(x)在(0,1)上为减函数,在(1,+∞)上为增函数
∴h(x)≥h(1)=2e,且x→+∞时,h(x)→+∞;x→0时,h(x)→+∞
即h(x)值域为[2e,+∞),
∴a≥2e时,方程a=
| 2ex0 |
| x0 |
∴a≥2e时,y=f(x)的图象上存在两点关于原点对称.
点评:本题考察了函数的单调性,函数的最值问题,导数的应用,函数图象的对称性,是一道综合题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
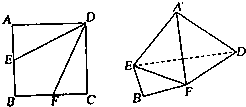 如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△ADE,△CDF分别沿DE,DF折起,使A,C两点重合于点A′.