题目内容
10．已知半径为10cm的圆上，一条弧所对的圆心角为60°，则弧长为$\frac{10π}{3}$cm．分析 先把圆心角化为弧度数，代入扇形的弧长公式：l=α•r 求出弧长．
解答 解：圆心角为60°即$\frac{π}{3}$，由扇形的弧长公式得：弧长l=α•r=$\frac{π}{3}$×10=$\frac{10π}{3}$cm，
故答案为：$\frac{10π}{3}$．
点评 本题考查弧长公式的应用，要注意公式中的圆心角一定要用弧度来表示，不能用度数，属于基础题．
练习册系列答案
相关题目
1．如图，矩形ABCD中，AB=2，AD=1，E，F分别是BC，CD中点，则$\overrightarrow{AE}$•$\overrightarrow{AF}$=（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{{\sqrt{6}}}{4}$ | C． | $\frac{5}{2}$ | D． | 4 |
5．函数f（x）=$\frac{A}{sin（ωx+φ）}（A＞0，ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，则$f（\frac{3π}{2}）$=（ ）
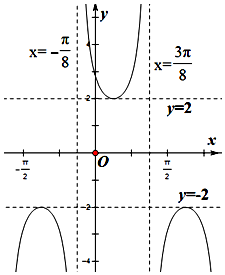
| A． | $2\sqrt{3}$ | B． | $-2\sqrt{3}$ | C． | $2\sqrt{2}$ | D． | $-2\sqrt{2}$ |
15．若函数g（x+2）=2x2-3x，则g（3）的值是（ ）
| A． | 35 | B． | 9 | C． | -1 | D． | -13 |
2．已知全集U={1，2，3，4}，集合A={1，3，4}，B={2，3}，则A∩（∁UB）=（ ）
| A． | {2} | B． | {1，4} | C． | {3} | D． | {1，2，3，4} |
20．$\int_0^1{（{\sqrt{2x-{x^2}}-x}）dx}$等于（ ）
| A． | $\frac{π-2}{4}$ | B． | $\frac{π-2}{2}$ | C． | $\frac{π-1}{2}$ | D． | $\frac{π-1}{4}$ |