题目内容
18.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{2}}}{2}$,长轴长等于圆R:x2+(y-2)2=4的直径,过点P(0,1)的直线l与椭圆C交于A,B两点,与圆R交于M,N两点;(1)求椭圆C的方程;
(2)求证:直线RA,RB的斜率之和是定值,并求出该定值;
(3)求|AB|•|MN|的取值范围.
分析 (Ⅰ)根据椭圆的简单几何性质,求出a、b的值即可;
(Ⅱ)当直线l的斜率存在时,求出直线RA、RB的斜率之和即可证明结论成立;
(Ⅲ)讨论直线l的斜率是否存在,利用弦长公式以及转化法、基本不等式等求出|AB|•|MN|的取值范围.
解答 解:(Ⅰ)因为椭圆C长轴长等于圆R:x2+(y-2)2=4的直径,
所以2a=4,a=2; …(1分)
由离心率为$\frac{\sqrt{2}}{2}$,得e2=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$,
所以$\frac{{b}^{2}}{{a}^{2}}=\frac{{b}^{2}}{4}=\frac{1}{2}$,得b2=2;…(2分)
所以椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;…(3分)
(Ⅱ)当直线l的斜率存在时,设l的方程为y=kx+1,与$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$联立,
消去y,得(1+2k2)x2+4kx-2=0;
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{4k}{1+2{k}^{2}}$,x1x2=-$\frac{2}{1+2{k}^{2}}$,…(5分)
由R(0,2),得kRA+kRB=$\frac{{y}_{1}-2}{{x}_{1}}+\frac{{y}_{2}-2}{{x}_{2}}$=$\frac{k{x}_{1}-1}{{x}_{1}}+\frac{k{x}_{2}-1}{{x}_{2}}$
=2k-($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$)=2k-$\frac{{x}_{1}{+x}_{2}}{{x}_{1}{x}_{2}}$=0.…(7分)
所以直线RA,RB的斜率之和等于零;…(8分)
(Ⅲ)当直线l的斜率不存在时,|AB|=2$\sqrt{2}$,|MN|=4,|AB|•|MN|=8$\sqrt{2}$;…(9分)
当直线l的斜率存在时,
|AB|=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{(\frac{-4k}{1+2{k}^{2}})^{2}+4×\frac{2}{1+2{k}^{2}}}$
=$\sqrt{1+{k}^{2}}\frac{\sqrt{32{k}^{2}+8}}{1+2{k}^{2}}$
|MN|=2$\sqrt{4-(\frac{1}{\sqrt{1+{k}^{2}}})^{2}}$=2$\sqrt{\frac{4{k}^{2}+3}{1+2{k}^{2}}}$,…(11分)
所以|AB|•|MN|=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{32{k}^{2}+8}}{1+2{k}^{2}}$×2$\sqrt{\frac{4{k}^{2}+3}{1+{k}^{2}}}$
=4$\sqrt{2}$•$\frac{\sqrt{(4{k}^{2}+1)(4{k}^{2}+3)}}{1+2{k}^{2}}$;
因为直线l过点P(0,1),所以直线l与椭圆C和圆R均交于两点,
令1+2k2=t,则t≥1,
所以|AB|•|MN|=4$\sqrt{2}$•$\sqrt{\frac{(2t-1)(2t+1)}{{t}^{2}}}=4\sqrt{2}\sqrt{4-\frac{1}{{t}^{2}}}<8\sqrt{2}$,
又y=4$\sqrt{2}$•$\sqrt{4-\frac{1}{{t}^{2}}}$在t≥1时单调递增,
所以|AB|•|MN|=4$\sqrt{2}\sqrt{4-\frac{1}{{t}^{2}}}≥4\sqrt{6}$,
当且仅当t=1,k=0等号成立;…(13分)
综上,|AB|•|MN|的取值范围是[4$\sqrt{6}$,8$\sqrt{2}$].…(14分)
点评 本题考查了圆锥曲线的综合应用问题,也考查了数形结合思想、方程思想的应用问题,考查了计算能力与分析问题、解决问题的能力,是综合性题目.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2x-y+3=0 | B. | 2x-y-3=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
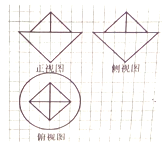 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$ | B. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$-8 | C. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$ | D. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$-8 |