题目内容
20．$\int_0^1{（{\sqrt{2x-{x^2}}-x}）dx}$等于（ ）| A． | $\frac{π-2}{4}$ | B． | $\frac{π-2}{2}$ | C． | $\frac{π-1}{2}$ | D． | $\frac{π-1}{4}$ |
分析 $\int_0^1{（{\sqrt{2x-{x^2}}-x}）dx}$=${∫}_{0}^{1}$$\sqrt{2x-{x}^{2}}$dx-${∫}_{0}^{1}$xdx，利用定积分的几何意义，即可得出结论．
解答 解：$\int_0^1{（{\sqrt{2x-{x^2}}-x}）dx}$=${∫}_{0}^{1}$$\sqrt{2x-{x}^{2}}$dx-${∫}_{0}^{1}$xdx=$\frac{1}{4}π$-$\frac{1}{2}{x}^{2}{|}_{0}^{1}$=$\frac{π-2}{4}$，
故选A．
点评 本题考查定积分知识，考查导数知识的运用，比较基础．
练习册系列答案
相关题目
8．
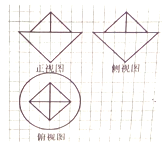如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（ ）| A． | 9（$\sqrt{2}$+1）π+8$\sqrt{3}$ | B． | 9（$\sqrt{3}$+2）π+4$\sqrt{3}$-8 | C． | 9（$\sqrt{3}$+2）π+4$\sqrt{3}$ | D． | 9（$\sqrt{2}$+1）π+8$\sqrt{3}$-8 |
15．某几何体的三视图如图，其正视图中的曲线部分为半圆，则该几何体的表面积为（ ）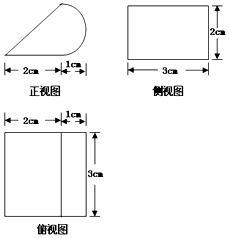
| A． | （19+π）cm2 | B． | （22+4π）cm2 | C． | （10+6$\sqrt{2}$+4π）cm2 | D． | （13+6$\sqrt{2}$+4π）cm2 |
5．经过点（-1，1），斜率是直线y=$\frac{\sqrt{2}}{2}$x-2的斜率的2倍的直线方程是（ ）
| A． | x=-1 | B． | y=1 | C． | y-1=$\sqrt{2}$（x+1） | D． | y-1=2$\sqrt{2}$（x+1） |
12．已知双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F（-2，0），过点F的直线交双曲线于AB两点．若AB的中点坐标为（-3，-1），则E的方程为（ ）
| A． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{1}$=1 | B． | $\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{3}$=1 | C． | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{1}$=1 | D． | $\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{9}$=1 |
9．命题“若a≥-1，则x+a≥1nx”的否定是（ ）
| A． | 若a＜-1，则x+a＜1nx | B． | 若a≥-1，则x+a＜1nx | ||
| C． | 若a＜-1，则x+a≥1nx | D． | 若a≥-1，则x+a≤1nx |