题目内容
已知函数f(x)=(a2-a+1)xa+2为幂函数,且为奇函数,设函数g(x)=f(x)+x.
(1)求实数a的值及函数g(x)的零点;
(2)是否存在自然数n,使g(n)=900?若存在,请求出n的值;若不存在,请说明理由.
(1)求实数a的值及函数g(x)的零点;
(2)是否存在自然数n,使g(n)=900?若存在,请求出n的值;若不存在,请说明理由.
考点:幂函数的性质
专题:函数的性质及应用
分析:(1)根据幂函数的定义,和奇函数的定义先求出a的值,再根据零点求法,零点转化为g(x)=0的实数根,解方程即可
(2)根据函数为增函数,然后验证f(9)=738,f(10)=1010,即可得出.
(2)根据函数为增函数,然后验证f(9)=738,f(10)=1010,即可得出.
解答:
解:(1)令a2-a+1=1,解得 a=0或a=1.…(1分)
当a=0时,f(x)=x2,它不是奇函数,不符合题意;
当a=1时,f(x)=x3,它是奇函数,符合题意.
所以a=1. …(3分)
此时g(x)=x3+x.
令g(x)=0,即 x3+x=0,解得 x=0.
所以函数g(x)的零点是x=0.…(5分)
(2)设函数y=x3,y=x.因为它们都是增函数,所以g(x)是增函数.…(7分)
又因为 g(9)=738,g(10)=1010. …(9分)
由函数的单调性,可知不存在自然数n,使g(n)=900成立. …(10分)
当a=0时,f(x)=x2,它不是奇函数,不符合题意;
当a=1时,f(x)=x3,它是奇函数,符合题意.
所以a=1. …(3分)
此时g(x)=x3+x.
令g(x)=0,即 x3+x=0,解得 x=0.
所以函数g(x)的零点是x=0.…(5分)
(2)设函数y=x3,y=x.因为它们都是增函数,所以g(x)是增函数.…(7分)
又因为 g(9)=738,g(10)=1010. …(9分)
由函数的单调性,可知不存在自然数n,使g(n)=900成立. …(10分)
点评:本题主要考查函数的零点与方程的实数根的联系,以及函数的单调性与函数值问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若实数x,y满足
,则
的最小值是( )
|
| y-3 |
| x-2 |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
如图是某样本数据的茎叶图,则该样本数据的众数为( )
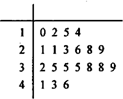

| A、10 | B、21 | C、35 | D、46 |
复数z=
,则z的共轭复数
在复平面内对应的点( )
| i2+i3+i4 |
| 1-i |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合M={x||x-1|<1},集合N={x|x2-2x<3},则M∩∁RN=( )
| A、{x|0<x<2} |
| B、{x|-1<x<2} |
| C、{x|-1<x≤0或2≤x<3} |
| D、∅ |