题目内容
11.已知直线l的参数方程为$\left\{{\begin{array}{l}{x=m+t}\\{y=t}\end{array}}\right.$(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2-ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.(1)求m的值并写出曲线C的直角坐标方程;
(2)求$\frac{{|{FA}|}}{{|{FB}|}}+\frac{{|{FB}|}}{{|{FA}|}}$的值.
分析 (1)直线l的参数方程为$\left\{{\begin{array}{l}{x=m+t}\\{y=t}\end{array}}\right.$(t为参数),消去参数t可得普通方程.曲线C的极坐标方程为2ρ2-ρ2cos2θ=12.利用互化公式可得曲线C的直角坐标方程,可得其左焦点,即可得出m.
(2)直线l的参数方程为$\left\{{\begin{array}{l}{x=-2\sqrt{2}+\frac{{\sqrt{2}}}{2}t'}\\{y=\frac{{\sqrt{2}}}{2}t'}\end{array}}\right.$,与曲线C的方程$\frac{x^2}{12}+\frac{y^2}{4}=1$联立,利用根与系数的关系、弦长公式即可得出.
解答 解:(1)直线l的参数方程为$\left\{{\begin{array}{l}{x=m+t}\\{y=t}\end{array}}\right.$(t为参数),消去参数t可得普通方程:x-y=m.
曲线C的极坐标方程为2ρ2-ρ2cos2θ=12.可得曲线C的直角坐标方程:2(x2+y2)-(x2-y2)=12,
∴曲线C的标准方程为$\frac{x^2}{12}+\frac{y^2}{4}=1$,则其左焦点为$({-2\sqrt{2},0})$,
故$m=-2\sqrt{2}$,曲线C的方程$\frac{x^2}{12}+\frac{y^2}{4}=1$.
(2)直线l的参数方程为$\left\{{\begin{array}{l}{x=-2\sqrt{2}+\frac{{\sqrt{2}}}{2}t'}\\{y=\frac{{\sqrt{2}}}{2}t'}\end{array}}\right.$,与曲线C的方程$\frac{x^2}{12}+\frac{y^2}{4}=1$联立,
得t'2-2t'-2=0,则|FA|•|FB|=|t'1t'2|=2,
$|{FA}|+|{FB}|=|{{{t'}_1}-{{t'}_2}}|=\sqrt{{{({{{t'}_1}+{{t'}_2}})}^2}-4{{t'}_1}{{t'}_2}}=2\sqrt{3}$,
故$\frac{{|{FA}|}}{{|{FB}|}}+\frac{{|{FB}|}}{{|{FA}|}}=\frac{{{{({|{FA}|+|{FB}|})}^2}}}{{|{FB}|•|{FA}|}}-2=4$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、一元二次方程的根与系数的关系、弦长公式,考查了推理能力与计算能力,属于中档题.

| A. | (-∞,4) | B. | (-∞,4] | C. | (-∞,5) | D. | (-∞,5] |

| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{1}{2}$ |
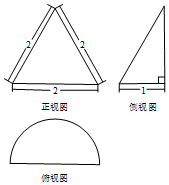
| A. | $\frac{{\sqrt{3}π}}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{{\sqrt{3}π}}{6}$ | D. | $\frac{{\sqrt{3}π}}{3}$ |
| A. | $({0,\frac{1}{a_3}})$ | B. | $({0,\frac{2}{a_3}})$ | C. | $({0,\frac{1}{a_1}})$ | D. | $({0,\frac{2}{a_1}})$ |
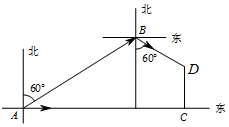 如图,船甲以每小时30公里的速度向正东航行,船甲在A处看到另一船乙在北偏东60°的方向上的B处,且$AB=30\sqrt{3}$公里,正以每小时$5\sqrt{3}$公里的速度向南偏东60°的方向航行,行驶2小时后,甲、乙两船分别到达C、D处,则CD等于$10\sqrt{3}$公里.
如图,船甲以每小时30公里的速度向正东航行,船甲在A处看到另一船乙在北偏东60°的方向上的B处,且$AB=30\sqrt{3}$公里,正以每小时$5\sqrt{3}$公里的速度向南偏东60°的方向航行,行驶2小时后,甲、乙两船分别到达C、D处,则CD等于$10\sqrt{3}$公里.