题目内容
 某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题:
某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题:| 分组 | 频数 | 频率 | |
| 第1组 | [60,70) | M | 0.26 |
| 第2组 | [70,80) | 15 | p |
| 第3组 | [80,90) | 20 | 0.40 |
| 第4组 | [90,100] | N | q |
| 合计 | 50 | 1 | |
(Ⅱ)若成绩在90分以上的学生获得一等奖,试估计全校所有参赛学生获一等奖的人数;
(Ⅲ)现从所有一等奖的学生中随机选择2名学生接受采访,已知一等奖获得者中只有2名女生,求恰有1名女生接受采访的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据频率分布表求出出M、N、p、q,再作出频率分布直方图;
(Ⅱ)若根据一等奖的概率为0.04,即可试估计全校所有参赛学生获一等奖的人数;
(Ⅲ)记获一等奖的6人为a,b,c,d,e,f其中a,b为获一等奖的女生,从所有一等奖的同学中随机抽取2名同学共有15种情况,女生的人数恰好为1人共有8种情况,根据概率公式计算即可
(Ⅱ)若根据一等奖的概率为0.04,即可试估计全校所有参赛学生获一等奖的人数;
(Ⅲ)记获一等奖的6人为a,b,c,d,e,f其中a,b为获一等奖的女生,从所有一等奖的同学中随机抽取2名同学共有15种情况,女生的人数恰好为1人共有8种情况,根据概率公式计算即可
解答:
解:(Ⅰ)M=13,N=2,p=0.30,q=0.04,
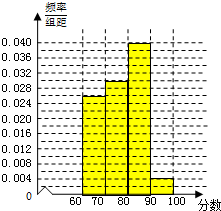
(Ⅱ)获一等奖的概率为0.04,获一等奖的人数估计为150×0.04=6(人)
(Ⅲ)记获一等奖的6人为a,b,c,d,e,f其中a,b为获一等奖的女生,
从所有一等奖的同学中随机抽取2名同学共有15种情况如下:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)15个等可能的结果,
女生的人数恰好为1人共有8种情况如下:(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f)
所以恰有1名女生接受采访的概率P=
.

(Ⅱ)获一等奖的概率为0.04,获一等奖的人数估计为150×0.04=6(人)
(Ⅲ)记获一等奖的6人为a,b,c,d,e,f其中a,b为获一等奖的女生,
从所有一等奖的同学中随机抽取2名同学共有15种情况如下:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)15个等可能的结果,
女生的人数恰好为1人共有8种情况如下:(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f)
所以恰有1名女生接受采访的概率P=
| 8 |
| 15 |
点评:本题考查了频率分布表与频率分布直方图以及古典概型的概率计算,考查了学生的运算能力与作图能力.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
函数f(x)=sin(2x+
)则下列结论正确的是( )
| π |
| 3 |
A、f(x)图象关于直线x=
| ||
B、f(x)图象关于(
| ||
C、f(x)图象向左平移
| ||
D、f(x)在(0,
|
如图程序,当输入变量x的值为5时,电脑屏幕上将显示( )


| A、5 | B、-5 |
| C、x=5 | D、x=-5 |