题目内容
函数f（x）=sin（2x+
）则下列结论正确的是（ ）
| π |
| 3 |
A、f（x）图象关于直线x=
| ||
B、f（x）图象关于（
| ||
C、f（x）图象向左平移
| ||
D、f（x）在（0，
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：分别根据函数的对称性，单调性和周期性的性质进行判断即可得到结论．
解答：
解：A．f（
）=sin（2×
+
）=sinπ=0，不是最值，∴f（x）的图象关于直线x=
对称错误；
B．f（
）=sin（2×
+
）=cos
≠0，∴f（x）的图象关于关于点（
，0）对称，错误；
C．∵f（x）图象向左平移
个单位，得到函数g（x）=sin[2（x+
）+
]=cos2x的图象，故C正确；
D．由-
+2kπ≤2x+
≤
+2kπ，k∈Z．得-
+kπ≤x≤
+kπ，k∈Z．
取k=0，可知f（x）在[-
，
]上为增函数，x超过
时递减，∴选项D不正确．
故选：C．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
B．f（
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| π |
| 4 |
C．∵f（x）图象向左平移
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
D．由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
取k=0，可知f（x）在[-
| 5π |
| 12 |
| π |
| 12 |
| π |
| 12 |
故选：C．
点评：本题主要考查三角函数的图象和性质，要求熟练掌握函数的对称性，周期性，单调性的性质的判断方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数y=1+sin（x-
）的图象（ ）
| π |
| 2 |
| A、关于x轴对称 | ||
| B、关于y轴对称 | ||
| C、关于原点对称 | ||
D、关于直线x=
|
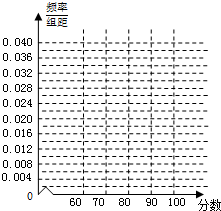某校有150名学生参加了中学生环保知识竞赛，为了解成绩情况，现从中随机抽取50名学生的成绩进行统计（所有学生成绩均不低于60分）．请你根据尚未完成的频率分布表，解答下列问题：已知直线l：（a+3）x+y-1=0，直线m：5x-5y+11=0，若直线l∥m，则直线l与直线m之间的距离是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|