题目内容
已知函数f(x)=2-x2+ax+3
(1)当a=0时,求函数f(x)的值域;
(2)若A={x|y=lg(5-x)},函数f(x)=2-x2+ax+3在A内是增函数,求a的取值范围.
(1)当a=0时,求函数f(x)的值域;
(2)若A={x|y=lg(5-x)},函数f(x)=2-x2+ax+3在A内是增函数,求a的取值范围.
考点:指数型复合函数的性质及应用
专题:函数的性质及应用
分析:(1)换元把函数可转化为:y=2t,t≤3,根据指数函数的单调性可判断:0<y≤23=8,
(2)根据复合函数的单调性判断g(x)=-x2+ax+3,在(-∞,5)是单调递增函数,即得出
≥5,求解即可a≥10.
(2)根据复合函数的单调性判断g(x)=-x2+ax+3,在(-∞,5)是单调递增函数,即得出
| a |
| 2 |
解答:
解:(1)当a=0时,函数f(x)=2 -x2+3,
令t(x)=3-x2,t≤3,
∴函数可转化为:y=2t,t≤3,
根据指数函数的单调性可判断:0<y≤23=8,
故函数f(x)的值域:(0,8].
(2)∵A={x|y=lg(5-x)},
∴A=(-∞,5),
∵函数f(x)=2-x2+ax+3在A内是增函数,
∴g(x)=-x2+ax+3,在(-∞,5)是单调递增函数,
即
≥5,a≥10
故a的取值范围:a≥10,
令t(x)=3-x2,t≤3,
∴函数可转化为:y=2t,t≤3,
根据指数函数的单调性可判断:0<y≤23=8,
故函数f(x)的值域:(0,8].
(2)∵A={x|y=lg(5-x)},
∴A=(-∞,5),
∵函数f(x)=2-x2+ax+3在A内是增函数,
∴g(x)=-x2+ax+3,在(-∞,5)是单调递增函数,
即
| a |
| 2 |
故a的取值范围:a≥10,
点评:本题综合考查了指数函数,二次函数的单调性,运用求解问题,属于中档题,关键是等价转化.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
函数y=1+sin(x-
)的图象( )
| π |
| 2 |
| A、关于x轴对称 | ||
| B、关于y轴对称 | ||
| C、关于原点对称 | ||
D、关于直线x=
|
已知直线l:(a+3)x+y-1=0,直线m:5x-5y+11=0,若直线l∥m,则直线l与直线m之间的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=cos(2x-
)的一条对称轴方程为( )
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
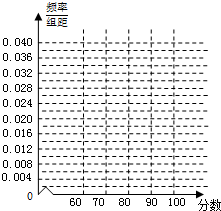 某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题:
某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题: