题目内容
已知方程x5+x+1=0和x+
+1=0的实根分别为α和β，则α+β= ．
| 5 | x |
考点：二次函数的性质
专题：函数的性质及应用
分析：解：令f（x）=x5+x+1，故f′（x）=5x4+1＞0，推出函数f（x）=x5+x+1在R上递增，进一步推出方程x5+x+1=0只有一个根，
由条件α5+α+1=0、β+
+1=0，推出α=
，α+β=
+β=-1．
由条件α5+α+1=0、β+
| 5 | β |
| 5 | β |
| 5 | β |
解答：
解：令f（x）=x5+x+1，
∴f′（x）=5x4+1＞0，∴函数f（x）=x5+x+1在R上递增，∴函数f（x）=x5+x+1在R上只有一个零点，
∴方程x5+x+1=0只有一个根，
∵方程x5+x+1=0和x+
+1=0的实根分别为α和β，
∴α5+α+1=0、β+
+1=0，
进一步有β+
=-1，
而β+
+1=0?(
)5+
+1=0，
故α5+α+1=0、(
)5+
+1=0，
而方程x5+x+1=0只有一个根，∴α=
∴α+β=
+β=-1
故答案为：-1
∴f′（x）=5x4+1＞0，∴函数f（x）=x5+x+1在R上递增，∴函数f（x）=x5+x+1在R上只有一个零点，
∴方程x5+x+1=0只有一个根，
∵方程x5+x+1=0和x+
| 5 | x |
∴α5+α+1=0、β+
| 5 | β |
进一步有β+
| 5 | β |
而β+
| 5 | β |
| 5 | β |
| 5 | β |
故α5+α+1=0、(
| 5 | β |
| 5 | β |
而方程x5+x+1=0只有一个根，∴α=
| 5 | β |
∴α+β=
| 5 | β |
故答案为：-1
点评：本题主要考查函数的零点与方程的根之间的关系，推导两个方程之间的关系是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
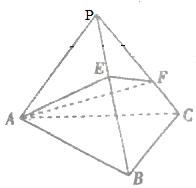如图，在三棱锥P-ABC中，三个侧面都是顶角为20°的等腰三角形，侧棱长均为a，E、F分别是PB、PC上的点，则△AEF周长的最小值为（ ）