题目内容
8. 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=1,DE=5.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=1,DE=5.(1)求棱锥C-ADE的体积;
(2)求证:平面ACE⊥平面CDE;
(3)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出$\frac{EF}{ED}$的值;若不存在,说明理由.
分析 (1)在Rt△ADE中,AE,可得S△ADE.由于CD⊥平面ADE,可得VC-ADE=$\frac{1}{3}$CD•S△ADE.
(2)由CD⊥平面ADE,可得CD⊥AE,进而得到AE⊥平面CDE,即可证明平面ACE⊥平面CDE;
(3)在线段DE上存在一点F,使AF∥平面BCE,$\frac{EF}{ED}=\frac{1}{6}$.设F为线段DE上一点,且$\frac{EF}{ED}=\frac{1}{6}$.过F作FM∥CD交CE于点M,由线面垂直的性质可得:CD∥AB.得四边形ABMF是平行四边形,于是AF∥BM,即可证明AF∥平面BCE.
解答  解:(1)在Rt△ADE中,$AE=\sqrt{A{D^2}-D{E^2}}=3\sqrt{11}$,
解:(1)在Rt△ADE中,$AE=\sqrt{A{D^2}-D{E^2}}=3\sqrt{11}$,
∵CD⊥平面ADE,
∴棱锥C-ADE的体积为:${V_{C-ADE}}=\frac{1}{3}{S_{△ADE}}•CD=\frac{1}{3}•\frac{AE•DE}{2}•CD=3\sqrt{11}$;…(4分)
(2)∵CD⊥平面ADE,AE?平面ADE,
∴CD⊥AE,
又∵AE⊥DE,CD∩DE=D,
∴AE⊥平面CDE,
又∵AE?平面ACE,
∴平面ACE⊥平面CDE;…(8分)
(3)结论:在线段DE上存在一点F,且$\frac{EF}{ED}=\frac{1}{6}$,使AF∥平面BCE,
设F为线段DE上一点,且$\frac{EF}{ED}=\frac{1}{6}$,过点F作FM∥CD交CE于M,则$FM=\frac{1}{6}CD$,
∵CD⊥平面ADE,AB⊥平面ADE,
∴CD∥AB,
又∵CD=6AB,
∴MF=AB,FM∥AB,
∴四边形ABMF是平行四边形,则AF∥BM,
又∵AF?平面BCE,BM?平面BCE,
∴AF∥平面BCE.…(12分)
点评 本题考查了线面面面垂直与平行的判定与性质定理、三棱锥的体积计算公式、平行线分线段成比例定理,考查了推理能力与计算能力,属于中档题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | 8 | B. | 7 | C. | 6 | D. | 3 |
| A. | f(x1)<f(x2) | B. | f(x1)>f(x2) | C. | f(x1)=f(x2) | D. | 不确定 |
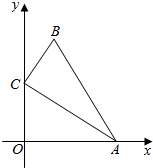 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是( )
如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是( )| A. | 3 | B. | $\sqrt{6}$ | C. | $1+\sqrt{2}$ | D. | $\sqrt{5}$ |
| A. | 若a≠0或b≠0,则a2+b2≠0 | B. | 若a2+b2≠0,则a≠0且b≠0 | ||
| C. | 若a2+b2≠0,则a≠0或b≠0 | D. | 若a=0且b=0,则a2+b2≠0 |
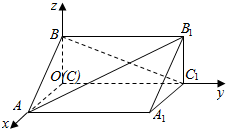 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )| A. | $\frac{4\sqrt{35}}{35}$ | B. | $\frac{\sqrt{35}}{70}$ | C. | $\frac{2\sqrt{35}}{35}$ | D. | $\frac{2}{35}$ |
