题目内容
3.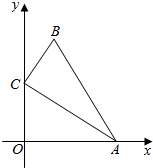 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是( )
如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是( )| A. | 3 | B. | $\sqrt{6}$ | C. | $1+\sqrt{2}$ | D. | $\sqrt{5}$ |
分析 Rt△AOC的外接圆圆心是AC中点,设AC中点为D,根据三角形三边关系有OB≤OD+BD=1+$\sqrt{2}$,即O、D、B三点共线时OB取得最大值.
解答  解:作AC的中点D,连接OD、BD,
解:作AC的中点D,连接OD、BD,
∵OB≤OD+BD,
∴当O、D、B三点共线时OB取得最大值,
∵BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,OD=AD=$\frac{1}{2}$AC=1,
∴点B到原点O的最大距离为1+$\sqrt{2}$.
故选:C.
点评 本题考查零点减距离的求法,最值的应用,能够理解在什么情况下,点B到原点O的距离最大是解题的关键.

练习册系列答案
相关题目
15.直线l:x-ty-1=0将圆(x-3)2+(y-3)2=4的弧长恰好分成1:2两部分,则此时的弦长为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
12.函数f(x)=log2x在区间$[{\frac{1}{2},2}]$上的最小值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
13.已知函数f(x)=$\left\{\begin{array}{l}{ln(x+1),}&{0<x≤2}\\{1-{2}^{x},}&{-2≤x≤0}\end{array}\right.$,若g(x)=|f(x)|-kx-k有3个零点,则实数k的取值范围是( )
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | D. | [$\frac{ln3}{3}$,$\frac{1}{e}$) |
 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=1,DE=5.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=1,DE=5. 如图是用条件语句编写的一个程序:若输入4,则输出的结果是15,该程序的功能是求函数$y=\left\{{\begin{array}{l}{{x^2}-1}\\ 2\\{2x}\end{array}}\right.,\begin{array}{l}{x>3}\\{x=3}\\{x<3}\end{array}$的值.
如图是用条件语句编写的一个程序:若输入4,则输出的结果是15,该程序的功能是求函数$y=\left\{{\begin{array}{l}{{x^2}-1}\\ 2\\{2x}\end{array}}\right.,\begin{array}{l}{x>3}\\{x=3}\\{x<3}\end{array}$的值.