题目内容
18.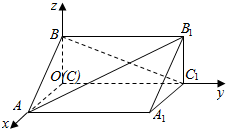 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )| A. | $\frac{4\sqrt{35}}{35}$ | B. | $\frac{\sqrt{35}}{70}$ | C. | $\frac{2\sqrt{35}}{35}$ | D. | $\frac{2}{35}$ |
分析 以C为原点,CA为x轴,CC1为y轴,CB为z轴,建立空间直角坐标系,利用向量法能求出直线BC1与直线AB1夹角的余弦值.
解答 解:以C为原点,CA为x轴,CC1为y轴,CB为z轴,建立空间直角坐标系,
∵CA=2CB,CC1=3CB,∴设CB=1,
得B(0,0,1),C1(0,3,0),A(2,0,0),B1(0,3,1),
$\overrightarrow{B{C}_{1}}$=(0,3,-1),$\overrightarrow{A{B}_{1}}$=(-2,3,1),
cos<$\overrightarrow{B{C}_{1}}$,$\overrightarrow{A{B}_{1}}$>=$\frac{\overrightarrow{B{C}_{1}}•\overrightarrow{A{B}_{1}}}{|\overrightarrow{B{C}_{1}}|•|\overrightarrow{A{B}_{1}}|}$=$\frac{9-1}{\sqrt{10}×\sqrt{14}}$=$\frac{4\sqrt{35}}{35}$.
∴直线BC1与直线AB1夹角的余弦值为$\frac{4\sqrt{35}}{35}$.
故选:A.
点评 本题考查两异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{ln(x+1),}&{0<x≤2}\\{1-{2}^{x},}&{-2≤x≤0}\end{array}\right.$,若g(x)=|f(x)|-kx-k有3个零点,则实数k的取值范围是( )
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | D. | [$\frac{ln3}{3}$,$\frac{1}{e}$) |
7.若直线2x-y-4=0在x轴和y轴上的截距分别为a和b,则a-b的值为( )
| A. | 6 | B. | 2 | C. | -2 | D. | -6 |
 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=1,DE=5.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=1,DE=5. 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点.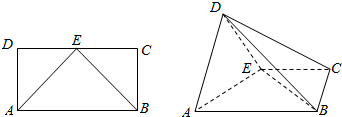 如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.
如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.