题目内容
函数f(x)=cosx-
sinx的一条对称轴方程是( )
| 3 |
A、x=
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:原式可化简为:f(x)=2cos(x+
),由余弦函数的图象可求其对称轴方程,再把选项逐一比较即可求解.
| π |
| 3 |
解答:
解:f(x)=cosx-
sinx=2cos(x+
)
对称轴方程为:x+
=2kπ,k∈Z
即有x=2kπ-
,k∈Z
不妨取k=0,有x=-
故选:C.
| 3 |
| π |
| 3 |
对称轴方程为:x+
| π |
| 3 |
即有x=2kπ-
| π |
| 3 |
不妨取k=0,有x=-
| π |
| 3 |
故选:C.
点评:本题主要考察了余弦函数的图象及其性质,属于基础题.

练习册系列答案
相关题目
设f(n)=2+24+27+210+…+23n+10(n∈N),则f(n)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线平分圆x2+y2-2x-4y+1=0的周长,则此直线的方程可能是( )
| A、x-y+1=0 |
| B、x+y+3=0 |
| C、x+y-1=0 |
| D、x-y+3=0 |
已知集合M={a2,a}.P={-a,2a-1};若card(M∪P)=3,则M∩P=( )
| A、{-1} | B、{1} |
| C、{0} | D、{3} |
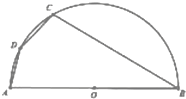 如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游
如图,半圆O是一个湖面的平面示意图,其直径AB=8百米,为了便与游