题目内容
数列{an}是公比为-
的等比数列,{bn}是首项为12的等差数列.现已知a9>b9且a10>b10,则以下结论中一定成立的是 .(请填写所有正确选项的序号).
①a9•a10<0;
②b10>0;
③b9>b10;
④a9>a10.
| 2 |
| 3 |
①a9•a10<0;
②b10>0;
③b9>b10;
④a9>a10.
考点:等差数列的性质,等比数列的性质
专题:等差数列与等比数列
分析:由等差数列和等比数列的性质,逐个判断可得.
解答:
解:∵数列{an}是公比为-
的等比数列,
∴a9•a10=a92•(-
)<0,①一定成立;
而④a9>a10,只有当a9为正数才成立,不一定成立;
又{bn}是首项为12的等差数列,a9>b9且a10>b10,
可得等差数列{bn}一定是递减数列,③一定成立;
②当公差很小时不成立;
故答案为:①③
| 2 |
| 3 |
∴a9•a10=a92•(-
| 2 |
| 3 |
而④a9>a10,只有当a9为正数才成立,不一定成立;
又{bn}是首项为12的等差数列,a9>b9且a10>b10,
可得等差数列{bn}一定是递减数列,③一定成立;
②当公差很小时不成立;
故答案为:①③
点评:本题考查等差数列和等比数列的性质,涉及数列的增减性,属中档题.

练习册系列答案
相关题目
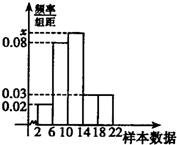 为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )
为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量1000的频率分布直方图如图所示,则样本数据落在[6,14)内的频数为( )| A、780 | B、660 |
| C、680 | D、460 |
已知sinα=-
,则cos(
-α)的值等于( )
| 1 |
| 3 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|