题目内容
3.矩形OABC的四个顶点坐标依次为$O({0,0}),A({\frac{π}{2},0}),B({\frac{π}{2},1}),C({0,1})$,线段OA,OC及$y=cosx({0<x≤\frac{π}{2}})$的图象围成的区域为Ω,若矩形OABC内任投一点M,则点M落在区域内Ω的概率为$\frac{2}{π}$.分析 根据题意,求解出线段OA,OC及$y=cosx({0<x≤\frac{π}{2}})$的图象围成的区域面积Ω和矩形OABC的面积可得点M落在区域内Ω的概率.
解答 解:由题意:线段OA,OC及$y=cosx({0<x≤\frac{π}{2}})$的图象围成的区域面积Ω=$-{∫}_{0}^{\frac{π}{2}}cosdx$=${sinx|}_{0}^{\frac{π}{2}}$=1,
矩形OABC的面积S=$\frac{π}{2}×1=\frac{π}{2}$.
点M落在区域内Ω的概率为:1$÷\frac{π}{2}=\frac{2}{π}$.
故答案为:$\frac{2}{π}$.
点评 本题考查了古典型概率问题,利用了定积分求面积.属于基础题.

练习册系列答案
相关题目
14.设i是虚数单位,复数i(1+ai)为纯虚数,则实数a为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
18.已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0),B(m,0)(m>0).若圆上存在点P使得$\overrightarrow{PA}•\overrightarrow{PB}=0$,则m的取值范围是( )
| A. | (-∞,4] | B. | (6,+∞) | C. | (4,6) | D. | [4,6] |
8.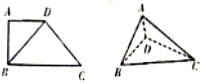 如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
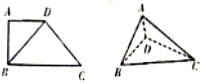 如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )| A. | 平面ABD⊥平面ABC | B. | 平面ACD⊥平面BCD | C. | 平面ABC⊥平面BCD | D. | 平面ACD⊥平面ABC |
15.已知直线l:y=k(x+$\sqrt{3}$)和圆C:x2+(y-1)2=1,若直线l与圆C相切,则k=( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$或0 | D. | $\sqrt{3}$或0 |
12.抛物线x2=4y的焦点到准线的距离为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |