题目内容
18.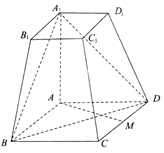 如图所示,在四棱台ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2.
如图所示,在四棱台ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2.(Ⅰ)若M为CD中点,求证:AM⊥平面AA1B1B;
(Ⅱ)求直线DD1与平面A1BD所成角的正弦值.
分析 (Ⅰ)推导出AM⊥CD,AM⊥AB,AM⊥AA1,由此能证明AM⊥平面AA1B1B
(Ⅱ)分别以AB,AM,AA1为x轴、y轴、z轴,建立如图所示的空间直角坐标系A-xyz,利用向量法能求出直线DD1与平面A1BD所成角θ的正弦值.
解答 证明:(Ⅰ)∵四边形为菱形,∠BAD=120°,连结AC,
∴△ACD为等边三角形,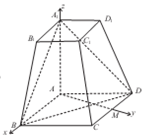
又∵M为CD中点,∴AM⊥CD,
由CD∥AB得,∴AM⊥AB,
∵AA1⊥底面ABCD,AM?底面ABCD,∴AM⊥AA1,
又∵AB∩AA1=A,∴AM⊥平面AA1B1B
解:(Ⅱ)∵四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2,
∴DM=1,$AM=\sqrt{3}$,∠AMD=∠BAM=90°,
又∵AA1⊥底面ABCD,
分别以AB,AM,AA1为x轴、y轴、z轴,建立如图所示的空间直角坐标系A-xyz,
则A1(0,0,2)、B(2,0,0)、$D({-1,\sqrt{3},0})$、${D_1}({-\frac{1}{2},\frac{{\sqrt{3}}}{2},2})$,
∴$\overrightarrow{D{D_1}}=({\frac{1}{2},-\frac{{\sqrt{3}}}{2},2})$,$\overrightarrow{BD}=({-3,\sqrt{3},0})$,$\overrightarrow{{A_1}B}=({2,0,-2})$,
设平面A1BD的一个法向量$\vec n=({x,y,z})$,
则有$\left\{\begin{array}{l}\vec n•\overrightarrow{BD}=0\\ \vec n•\overrightarrow{{A_1}B}=0\end{array}\right.⇒\left\{\begin{array}{l}-3x+\sqrt{3}y=0\\ 2x-2z=0\end{array}\right.⇒y=\sqrt{3}x=\sqrt{3}z$,令x=1,则$\vec n=({1,\sqrt{3},1})$,
∴直线DD1与平面A1BD所成角θ的正弦值:
$sinθ=|{cos<\vec n,\overrightarrow{D{D_1}}>}|=|{\frac{{\vec n•\overrightarrow{D{D_1}}}}{{|{\vec n}|•|{\overrightarrow{D{D_1}}}|}}}|=\frac{1}{5}$.
点评 本题考查线面垂直的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
| A. | $\frac{3}{2}+\frac{3}{2}i$ | B. | $\frac{1}{2}-\frac{3}{2}i$ | C. | $\frac{1}{2}+\frac{3}{2}i$ | D. | $\frac{3}{2}-\frac{3}{2}i$ |
| A. | {2,3,4} | B. | {1,2,3,4,5} | C. | {2,3} | D. | T |
| A. | {x|-ln3<x<ln3} | B. | {x|x<-ln3,或x>ln3} | ||
| C. | {x|-ln3<x<0,或x>ln3} | D. | {x|x<-ln3,或0<x<ln3} |
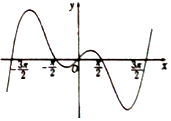
| A. | f(x)=x+sinx | B. | f(x)=$\frac{cosx}{x}$ | C. | f(x)=x(x-$\frac{π}{2}$)(x-$\frac{3π}{2}$) | D. | f(x)=xcosx |
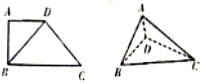 如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使得平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体中,下列说法正确的是( )| A. | 平面ABD⊥平面ABC | B. | 平面ACD⊥平面BCD | C. | 平面ABC⊥平面BCD | D. | 平面ACD⊥平面ABC |