题目内容
已知等差数列{an}前三项的和为-3,前三项的积为8.
(1)求等差数列{an}的通项公式;
(2)若a2、a3、a1成等比数列,求数列{|an|}的前n项和.
(1)设等差数列{an}的公差为d,则a2=a1+d,a3=a1+2d,
由题意得
解得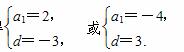
所以由等差数列通项公式可得an=2-3(n-1)=-3n+5,或an=-4+3(n-1)=3n-7.
故an=-3n+5,或an=3n-7.
(2)当an=-3n+5时,a2,a3,a1分别为-1,-4,2,不成等比数列;
当an=3n-7时,a2,a3,a1分别为-1,2,-4,成等比数列,满足条件.
故|an|=|3n-7|=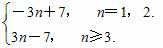
记数列{|an|}的前n项和为Sn.
当n=1时,S1=|a1|=4;
当n=2时,S2=|a1|+|a2|=5;
当n≥3时,
Sn=S2+|a3|+|a4|+…+|an|=5+(3×3-7)+(3×4-7)+…+(3n-7)
=5+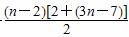 =
=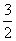 n2-
n2-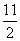 n+10.
n+10.
当n=2时,满足此式.
综上,Sn=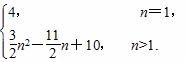

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的最小值为________.
的最小值为________.
 ,则它们的第7项之比为________.
,则它们的第7项之比为________.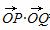 等于( )
等于( )