题目内容
已知等差数列{an}首项为a,公差为b,等比数列{bn}首项为b,公比为a,其中a、b都是大于1的正整数,且a1<b1,b2<a3,那么a=________;若对于任意的n∈N*,总存在m∈N*,使得bn=am+3成立,则an=________.
2 5n-3
[解析] 由已知条件可得
若a=2,显然符合条件;若a>2,则a<b< ,解得a<3,即2<a<3,即不存在a满足条件,由此可得a=2.
,解得a<3,即2<a<3,即不存在a满足条件,由此可得a=2.
当a=2时,an=2+(n-1)b,bn=b×2n-1,若存在m∈N*,使得bn=am+3成立,则b×2n-1=2+(m-1)b+3,即得b×2n-1=bm+5-b,当b=5时,方程2n-1=m总有解,此时an=5n-3.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
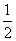 ,an+1=1-
,an+1=1-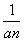 (n≥2),则a2014=________.
(n≥2),则a2014=________.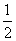 (log0.5a5+log0.5a7),Q=log0.5
(log0.5a5+log0.5a7),Q=log0.5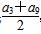 ,P与Q的大小关系是( )
,P与Q的大小关系是( )
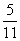 ,则数列{an}的通项公式为( )
,则数列{an}的通项公式为( )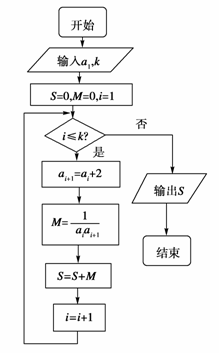
 =|ad-bc|,则不等式log
=|ad-bc|,则不等式log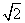
 <0的解集为________.
<0的解集为________.