题目内容
设Sn表示数列{an}的前n项和.
(1)若{an}是等差数列,推导Sn的计算公式;
(2)若a1=1,q≠0,且对所有正整数n,有Sn=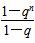 .判断{an}是否为等比数列,并证明你的结论.
.判断{an}是否为等比数列,并证明你的结论.
(1)方法一:设{an}的公差为d,则
Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d],
又Sn=an+an-1+…+a1
=[a1+(n-1)d]+[a1+(n-2)d]+…+a1,
∴2Sn=[2a1+(n-1)d]+[2a1+(n-1)d]+…+[2a1+(n-1)d]=2na1+n(n-1)d,
∴Sn=na1+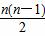 d.
d.
方法二:设{an}的公差为d,则
Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d],
又Sn=an+(an-d)+…+[an-(n-1)d],两式相加得2Sn=n(a1+an),
∴Sn= .
.
(2){an}是等比数列,证明如下:∵Sn=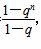 ,
,
∴an+1=Sn+1-Sn=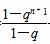 -
-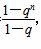 =
=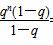 =qn.
=qn.
∵a1=1,q≠0,∴当n≥1时,有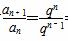 =q,
=q,
因此,{an}是首项为1且公比为q的等比数列.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
将正偶数按下表排成5列:
|
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 第1行 |
| 2 | 4 | 6 | 8 |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 |
| 18 | 20 | 22 | 24 |
| …… |
| …… | 28 | 26 |
那么2014应该在第________行第________列.
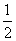 (log0.5a5+log0.5a7),Q=log0.5
(log0.5a5+log0.5a7),Q=log0.5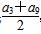 ,P与Q的大小关系是( )
,P与Q的大小关系是( )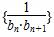 的前n项和Tn.
的前n项和Tn. ,a4=
,a4= (1+2x)dx,则公比q为________.
(1+2x)dx,则公比q为________.