题目内容
已知数列{an}的前n项和为Sn,点(an+2,Sn+1)在直线y=4x-5上,其中n∈N*.令bn=an+1-2an,且a1=1.
(1)求数列{bn}的通项公式;
(2)若f(x)=b1x+b2x2+b3x3+…+bnxn,求f ′(1)的表达式.
(1)∵Sn+1=4(an+2)-5,∴Sn+1=4an+3.
∴Sn=4an-1+3(n≥2),∴an+1=4an-4an-1(n≥2),
∴an+1-2an=2(an-2an-1)(n≥2).
∴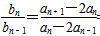 =2(n≥2).
=2(n≥2).
∴数列{bn}为等比数列,其公比为q=2,首项b1=a2-2a1,
而a1+a2=4a1+3,且a1=1,∴a2=6.
∴b1=6-2=4,∴bn=4×2n-1=2n+1.
(2)∵f(x)=b1x+b2x2+b3x3+…+bnxn,
∴f ′(1)=b1+2b2+3b3+…+nbn.
∴f ′(1)=22+2·23+3·24+…+n·2n+1①
∴2f ′(1)=23+2·24+3·25+…+n·2n+2②
①-②得-f ′(1)=22+23+24+…+2n+1-n·2n+2
=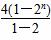 -n·2n+2=-4(1-2n)-n·2n+2,
-n·2n+2=-4(1-2n)-n·2n+2,
∴f ′(1)=4+(n-1)·2n+2.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
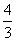 ) B.n(n-
) B.n(n- )
)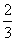 ) D.n(n-
) D.n(n-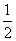 )
)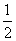 (log0.5a5+log0.5a7),Q=log0.5
(log0.5a5+log0.5a7),Q=log0.5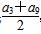 ,P与Q的大小关系是( )
,P与Q的大小关系是( )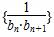 的前n项和Tn.
的前n项和Tn. ,a4=
,a4= (1+2x)dx,则公比q为________.
(1+2x)dx,则公比q为________. ,an+bn=1,bn+1=
,an+bn=1,bn+1= ,则b2014=( )
,则b2014=( ) B.
B. C.
C. D.
D.
 的最小值是( )
的最小值是( )