题目内容
如果复数z满足|z+1-i|=2,那么|z-2+i|的最大值是 .
考点:复数求模
专题:数系的扩充和复数
分析:设z=x+yi(x,y∈R),由复数的几何意义可知复数z对应点的轨迹为以A(-1,1)为圆心,2为半径的圆,再借助|z-2+i|的几何意义可求其最大值.
解答:
解:设z=x+yi(x,y∈R),
由|z+1-i|=2,知复数z对应点的轨迹为以A(-1,1)为圆心,2为半径的圆,
图形如下所示:
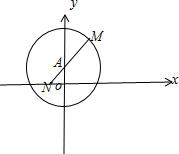
|z-2+i|表示复数z对应的点到N(2,-1)的距离,
易知该距离的最大值为|MN|的长,|MN|=
=
.
|z-2+i|的最大值是:2+
.
故答案为:2+
.
由|z+1-i|=2,知复数z对应点的轨迹为以A(-1,1)为圆心,2为半径的圆,
图形如下所示:
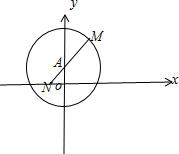
|z-2+i|表示复数z对应的点到N(2,-1)的距离,
易知该距离的最大值为|MN|的长,|MN|=
| (2+1)2+(-1-1)2 |
| 13 |
|z-2+i|的最大值是:2+
| 13 |
故答案为:2+
| 13 |
点评:本题考查复数求模、复数的几何意义,属基础题,正确理解复数的几何意义是解决该题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
正三角形ABC中,D,E分别是AB,AC的中点,则以B,C为焦点且过D,E的双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|