题目内容
7.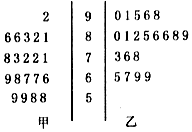 某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:(1)学校规定:成绩不得低于85分的为优秀,请填写如表的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
分析 (1)根据茎叶图,计算甲、乙两班不低于85分的学生数,填写列联表,
计算观测值K2,从而得出概率结论;
(2)用列举法计算从甲班成绩不得低于80分的6人中抽取2名的基本事件数,求出对应的概率值.
解答 解:(1)根据茎叶图,计算甲班不低于85分的学生数是有3人,乙班不低于85分有9人,
填写列联表,如下;
| 甲班 | 乙班 | 合计 | |
| 优秀 | 3 | 10 | 13 |
| 不优秀 | 17 | 10 | 27 |
| 合计 | 20 | 20 | 40 |
因此,“能在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关”
(2)甲班成绩不得低于80分的有6人,记为A、B、C、D、E、F,
其中86分有2人,记为E、F,
从这6人中随机抽取2名,基本事件是
AB、AC、AD、AE、AF、BC、BD、BE、BF、
CD、CE、CF、DE、DF、EF共15种,
成绩为86分的同学至少有一个被抽中的基本事件为
AE、AF、BE、BF、CE、CF、DE、DF、EF共9种,
故所求的概率为P=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查了茎叶图、列联表以及独立性检验和列举法球概率的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在△ABC中,角A、B均为锐角,则cosA>sinB是△ABC为钝角三角形的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
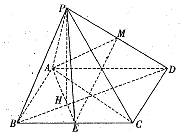 四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.