��Ŀ����
16��ij�Ƽ�������չ�������ܻ������� A��B��C��D �����ͺţ�ÿ���ͺ������� 4 ̨��Ҫ��ÿ λ������ֻ�ܹ���1̨ij���ͺŵĻ����ˣ��ҹ�����������һ���ͺŵĻ������ǵȿ��ܵģ������� 4 ����Ҫ��������ˣ������ڻ᳡չ��̨�ϣ�չ�����ѷź��� A��B��C��D �����ͺŵĻ����˸�һ̨���ְ����� �ų�һ�ű��ݽ�Ŀ���� A ���� B �������� C ���� D �Ͳ����ڵĸ��ʣ�
�������� 4 ���˹���Ļ����˵��ͺ�����Ϊ�Σ���� �ķֲ��к���ѧ������
���� ��I�� ���л����˵��ܵ�����Ϊ${A}_{4}^{4}$��A ���� B �������� C ���� D �Ͳ�����ֻ����C��AB��D����C��BA��D��C��DҲ���Խ�����
��II���εĿ���ȡֵΪ1��2��3��4��P����=1��=$\frac{{A}_{4}^{1}}{{4}^{4}}$��P����=2��=$\frac{{∁}_{4}^{2}��{2}^{4}-2��}{{4}^{4}}$��P����=4��=$\frac{{A}_{4}^{4}}{{4}^{4}}$��P����=3��=$\frac{{∁}_{4}^{3}{∁}_{4}^{2}{A}_{3}^{3}}{{4}^{4}}$�����ɵó���
��� �⣺��I�� A ���� B �������� C ���� D �Ͳ�����ֻ����C��AB��D����C��BA��D��C��DҲ���Խ�����
��˸���P=$\frac{{A}_{2}^{2}•{A}_{2}^{2}}{{A}_{4}^{4}}$=$\frac{1}{6}$��
��II���εĿ���ȡֵΪ1��2��3��4��
P����=1��=$\frac{{A}_{4}^{1}}{{4}^{4}}$=$\frac{4}{256}$��P����=2��=$\frac{{∁}_{4}^{2}��{2}^{4}-2��}{{4}^{4}}$=$\frac{84}{256}$��P����=4��=$\frac{{A}_{4}^{4}}{{4}^{4}}$=$\frac{24}{256}$��P����=3��=$\frac{{∁}_{4}^{3}{∁}_{4}^{2}{A}_{3}^{3}}{{4}^{4}}$=.$\frac{144}{256}$
��
| �� | 1 | 2 | 3 | 4 |
| P | $\frac{4}{256}$ | $\frac{84}{256}$ | $\frac{144}{256}$ | $\frac{24}{256}$ |
���� ���⿼������������ϵļ��㹫ʽ��������¼��ĸ��ʼ��㹫ʽ����������ķֲ�������ѧ������������������������������������е��⣮

| A�� | $\sqrt{2}+1$ | B�� | $\sqrt{7}+1$ | C�� | $\sqrt{2}$-1 | D�� | $\sqrt{7}$-1 |
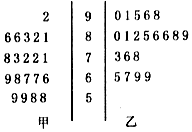 ij��ѧ�ߵ���ѧ��ʦ��ѧ�ڷֱ���A��B���ֲ�ͬ�Ľ�ѧ��ʽ����ס���������һ�°ࣨ������Ϊ60�ˣ���ѧ��ѧƽ�������������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20���ĸߵ���ѧ��ĩ���Գɼ����õ���Ҷͼ��ͼ��
ij��ѧ�ߵ���ѧ��ʦ��ѧ�ڷֱ���A��B���ֲ�ͬ�Ľ�ѧ��ʽ����ס���������һ�°ࣨ������Ϊ60�ˣ���ѧ��ѧƽ�������������ʶ���ͬ���ڷ̶ܳȺ��Ծ��Զ�һ�������������ȡ�ס��������20���ĸߵ���ѧ��ĩ���Գɼ����õ���Ҷͼ��ͼ����1��ѧУ�涨���ɼ����õ���85�ֵ�Ϊ���㣬����д�����2��2�����������жϡ��ܷ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�ɼ��������ѧ��ʽ�йأ���
| �װ� | �Ұ� | �ϼ� | |
| ���� | |||
| ������ | |||
| �ϼ� |
| P��k2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
��2���ִӼװ�ߵ���ѧ�ɼ����õ���80�ֵ�ͬѧ�������ȡ����ͬѧ����ɼ�Ϊ86�ֵ�ͬѧ������һ�������еĸ��ʣ�
| A�� | 0 | B�� | a | C�� | 2a+1 | D�� | -1 |
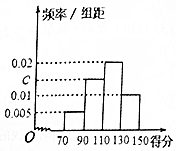 ijУΪ�˽�У��ȫ����ר���ij�Ч����ȫУ3000��ѧ������һ�ΰ�ȫ��ʶ���ԣ����ݲ��Գɼ����������㡱�������á������������������ĸ��ȼ����������ȡ����ѧ���Ĵ����ͳ�ƽ������Ӧ��Ƶ�ʷֲ�ֱ��ͼ������ʾ��
ijУΪ�˽�У��ȫ����ר���ij�Ч����ȫУ3000��ѧ������һ�ΰ�ȫ��ʶ���ԣ����ݲ��Գɼ����������㡱�������á������������������ĸ��ȼ����������ȡ����ѧ���Ĵ����ͳ�ƽ������Ӧ��Ƶ�ʷֲ�ֱ��ͼ������ʾ��| �ȼ� | ������ | ���� | ���� | ���� |
| �÷� | [70��90�� | [90��110�� | [110��130�� | [130��150] |
| Ƶ�� | 6 | a | 24 | b |
�����Թ��Ƹ�У��ȫ��ʶ��������Ϊ�����㡱��ѧ��������
������֪�Ѳ��÷ֲ�����ķ������������ȼ�Ϊ�����㡱�͡����á���ѧ������ѡ6�˽���ǿ����ѵ�����ٴ���6������ѡ2�˲μ��м�У��ȫ֪ʶ��������ѡȡ��2������1��Ϊ�����㡱�ĸ��ʣ�

| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
| A�� | ��1��3] | B�� | [3��+�ޣ� | C�� | ��0��3�� | D�� | ��0��3] |
| A�� | ���ɺ���g��x��=cos2x��ͼ������ƽ��$\frac{��}{3}$����λ���� | |
| B�� | ���ɺ���g��x��=cos2x��ͼ������ƽ��$\frac{��}{3}$����λ���� | |
| C�� | ���ɺ���g��x��=cos2x��ͼ������ƽ��$\frac{��}{6}$����λ���� | |
| D�� | ���ɺ���g��x��=cos2x��ͼ������ƽ��$\frac{��}{6}$����λ���� |