题目内容
19.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=3+tcosφ}\\{y=1+tsinφ}\end{array}\right.$(t为参数),在以坐标原点为极点,x轴的正半轴为极轴的极坐标中,圆C的方程为ρ=4cosθ.(Ⅰ)求l的普通方程和C的直角坐标方程;
(Ⅱ)当φ∈(0,π)时,l与C相交于P,Q两点,求|PQ|的最小值.
分析 (Ⅰ)利用三种方程的转化方法,求l的普通方程和C的直角坐标方程;
(Ⅱ)由(Ⅰ)可知圆心坐标为C(2,0),半径为2,直线过点A(3,1),CA⊥PQ时,可求|PQ|的最小值.
解答 解:(Ⅰ)直线l的参数方程为$\left\{\begin{array}{l}{x=3+tcosφ}\\{y=1+tsinφ}\end{array}\right.$(t为参数),普通方程为y-1=tanφ(x-3),
圆C的方程为ρ=4cosθ,直角坐标方程为x2+y2=4x;
(Ⅱ)由(Ⅰ)可知圆心坐标为C(2,0),半径为2,直线过点A(3,1),∴|CA|=$\sqrt{2}$,
∴CA⊥PQ时,|PQ|的最小值为2$\sqrt{4-2}$=2$\sqrt{2}$.
点评 本题考查三种方程的转化,考查直线与圆的位置关系,考查弦长的计算,属于中档题.

练习册系列答案
相关题目
9.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,若在双曲线上存在点P使△OPF2是以O为顶点的等腰三角形,又|PF1|+|PF2|=2$\sqrt{2{c}^{2}-{b}^{2}}$,其中c为双曲线的半焦距,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$-1 |
7.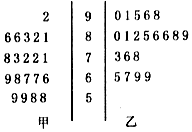 某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:
(1)学校规定:成绩不得低于85分的为优秀,请填写如表的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
下面临界值表仅供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
 某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:(1)学校规定:成绩不得低于85分的为优秀,请填写如表的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
14.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,如表记录了小李某月1号到5号每天打篮球的时间x(单位:小时)与当天投篮命中率y之间的关系:
(Ⅰ)求小李这5天的平均投篮命中率
(Ⅱ)用线性回归分析方法,预测小李该月6号打3.5小时篮球的投篮命中率(保留2位小数点)
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-{y}_{i})^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
| 时间x | 1 | 1.5 | 2 | 2.5 | 3 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(Ⅱ)用线性回归分析方法,预测小李该月6号打3.5小时篮球的投篮命中率(保留2位小数点)
参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-{y}_{i})^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
4.已知实数x,y满足$\left\{\begin{array}{l}{x≥0}\\{x-2y≥0}\\{y≥x-1}\end{array}\right.$,则z=ax+y(a>0)的最小值为( )
| A. | 0 | B. | a | C. | 2a+1 | D. | -1 |
11.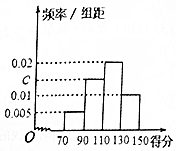 某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
(Ⅰ)求a,b,c的值;
(Ⅱ)试估计该校安全意识测试评定为“优秀”的学生人数;
(Ⅲ)已知已采用分层抽样的方法,从评定等级为“优秀”和“良好”的学生中任选6人进行强化培训,现再从这6人中任选2人参加市级校园安全知识竞赛,求选取的2人中有1人为“优秀”的概率.
 某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不及格 | 及格 | 良好 | 优秀 |
| 得分 | [70,90) | [90,110) | [110,130) | [130,150] |
| 频数 | 6 | a | 24 | b |
(Ⅱ)试估计该校安全意识测试评定为“优秀”的学生人数;
(Ⅲ)已知已采用分层抽样的方法,从评定等级为“优秀”和“良好”的学生中任选6人进行强化培训,现再从这6人中任选2人参加市级校园安全知识竞赛,求选取的2人中有1人为“优秀”的概率.