题目内容
18．已知正项等比数列{an}的第四项，第五项，第六项分别为1，m，9，则双曲线$C：\frac{y^2}{6}-\frac{x^2}{m}=1$的离心率为$\frac{\sqrt{6}}{2}$．分析 由正项等比数列{an}的第四项，第五项，第六项分别为1，m，9，求出m，由此入手能求出离心率．
解答 解：∵正项等比数列{an}的第四项，第五项，第六项分别为1，m，9，
∴m=3．
∴双曲线$C：\frac{y^2}{6}-\frac{x^2}{m}=1$的离心率为$\frac{3}{\sqrt{6}}$=$\frac{\sqrt{6}}{2}$．
故答案为：$\frac{\sqrt{6}}{2}$．
点评 本题考查圆锥曲线的离心率的求法，解题时要注意等比数列的性质的合理运用．
练习册系列答案
相关题目
8．记复数z的共轭复数为$\overline{z}$，若$\overline{z}$（1-i）=2i（i为虚数单位），则复数z的模|z|=（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | 2$\sqrt{2}$ | D． | 2 |
9．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，若在双曲线上存在点P使△OPF2是以O为顶点的等腰三角形，又|PF1|+|PF2|=2$\sqrt{2{c}^{2}-{b}^{2}}$，其中c为双曲线的半焦距，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{2}$+1 | C． | $\sqrt{3}$ | D． | $\sqrt{3}$-1 |
6．已知△ABC的三个顶点的坐标为A（0，1），B（1，0），C（0，-2），O为坐标原点，动点M满足|$\overrightarrow{CM}$|=1，则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OM}$|的最大值是（ ）
| A． | $\sqrt{2}+1$ | B． | $\sqrt{7}+1$ | C． | $\sqrt{2}$-1 | D． | $\sqrt{7}$-1 |
13．已知$a=\frac{1}{π}\int_{-1}^1{（\sqrt{1-{x^2}}+sinx）dx}$，则二项式${（2x-\frac{a}{x^2}）^9}$的展开式中的常数项为-672．
3．若复数z满足z-1=$\frac{（i-1）^{2}+2}{1+i}$（i为虚数单位），则z在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
7．
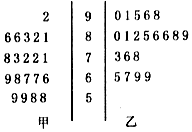某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班（人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）．现随机抽取甲、乙两班各20名的高等数学期末考试成绩，得到茎叶图如图：
（1）学校规定：成绩不得低于85分的为优秀，请填写如表的2×2列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
下面临界值表仅供参考：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
（2）现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学，求成绩为86分的同学至少有一个被抽中的概率．
某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班（人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）．现随机抽取甲、乙两班各20名的高等数学期末考试成绩，得到茎叶图如图：（1）学校规定：成绩不得低于85分的为优秀，请填写如表的2×2列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P（k2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（2）现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学，求成绩为86分的同学至少有一个被抽中的概率．