题目内容
19. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点.(Ⅰ)证明:MN∥平面PAB;
(Ⅱ)求证:平面PMC⊥平面PAD;
(Ⅲ)求直线AN与平面PMC所成角的正弦值.
分析 (1)取PB,BC中点E,F,连EN,AE,AF,由N为PC中点,说明EN∥BC,证明EN∥AM.推出MN∥AE,然后证明MN∥面PAB.
(2)说明AF⊥BC,证明CM⊥AD.推出CM⊥PA.证明CM⊥面PAD,然后证明面PMC⊥面PAD.
(3)过A作AG⊥PM,垂足为G.推出AG⊥面PMC,连接AN,GN.说明∠ANG为AN与平面PMC所成角.Rt△ANG中求解AN与平面PMC所成角正弦值即可.
解答 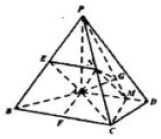 解:(1)证明:取PB,BC中点E,F,连EN,AE,AF,由N为PC中点,
解:(1)证明:取PB,BC中点E,F,连EN,AE,AF,由N为PC中点,
所以EN∥BC,且$EN=\frac{1}{2}BC=2$.由AM=2MD,AC=3,则AM=2,
又AD∥BC,则EN∥AM.
所以四边形ENMA为平行四边形,所以MN∥AE,且AE?面PAB,MN?面PAB,
则MN∥面PAB.
(2)证明:∵AB=AC,∴AF⊥BC,又AM∥FC,AM=FC=2所以四边形AFCM为平行四边形,故CM⊥AD.
又∵PA⊥面ABCD.CM?面ABCD,∴CM⊥PA.又AD∩PA=A,所以CM⊥面PAD,
∵CM?面ABCD,∴面PMC⊥面PAD.
(3)过A作AG⊥PM,垂足为G.由(2)知面PMC⊥面PAD,面PMC∩面PAD=PM,
AG?面PAD,∴AG⊥面PMC,连接AN,GN.
则GN为AN在平面PMC上的射影,∴∠ANG为AN与平面PMC所成角.
Rt△ANG中$AN=\frac{1}{2}PC$=$\frac{1}{2}\sqrt{P{A^2}+A{C^2}}=\frac{5}{2}$,
$AG=\frac{PA•AM}{{\sqrt{P{A^2}+A{M^2}}}}=\frac{{4\sqrt{5}}}{5}$,
$sin∠ANG=\frac{AG}{AN}=\frac{{8\sqrt{5}}}{25}$,
∴AN与平面PMC所成角正弦值为$\frac{{8\sqrt{5}}}{25}$.
点评 本题考查直线与平面所成角,直线与平面平行以及垂直的判定定理以及性质定理的应用,考查空间想象能力以及计算能力.

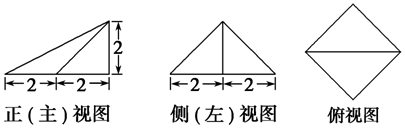
| A. | 2$\sqrt{2}$+2$\sqrt{6}$+8 | B. | 4$\sqrt{2}$+4$\sqrt{6}$+8 | C. | 8$\sqrt{2}$+8 | D. | 16 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
| A. | 有两个面平行,其余各面都是三角形的几何体叫棱柱 | |
| B. | 有两个面平行,其余各面都是梯形的几何体叫棱台 | |
| C. | 有一个面是多边形,其余各面都是五边形的几何体叫棱锥 | |
| D. | 棱台各侧棱的延长线交于一点 |
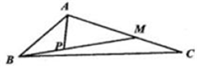 如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.
如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.