题目内容
15.已知等差数列{an}的前n项和Sn=-2n2-n(1)求通项an的表达式;
(2)说明{an}是一个怎样的等差数列;
(3)求a1+a3+a5+…+a25的值.
分析 (1)根据题意,由公式an=Sn-Sn-1可得an=-4n+1,进而利用a1=s1计算可得a1的值,验证可得a1=-3符合计算出的an公式,即可得答案;
(2)由(1)求出an公式,可得等差数列{an}的公差d=-4<0,由等差数列的性质可得答案;
(3)根据题意,由等差数列的性质:a1+a3+a5+…+a25=13a13,由(1)求出通项公式计算可得答案.
解答 解:(1)根据题意,等差数列{an}的前n项和Sn=-2n2-n
则an=Sn-Sn-1=(-2n2-n)-[-2(n-1)2-(n-1)]=-4n+1,
n=1时,a1=s1=-3,也符合an=-4n+1,
故数列{an}的通项公式为an=-4n+1;
(2)由(1)可得,等差数列{an}的通项公式为an=-4n+1,
其公差d=-4<0,
则该数列为递减的等差数列;
(3)根据题意,由等差数列的性质:
a1+a3+a5+…+a25=13a13=13×(-4×13+1)=-663.
点评 本题考查等差数列的性质,涉及等差数列的通项公式,关键是正确求出该数列的通项公式.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
10.己知三棱锥A-BCD的所有顶点都在球O的球面上,AB为球O的直径,若该三棱锥的体积为$\frac{4\sqrt{3}}{3}$.BC=4,BD=$\sqrt{3}$,∠CBD=90°,则球O的表面积为( )
| A. | 11π | B. | 20π | C. | 23π | D. | 35π |
4.定义在实数集R上函数y=f(x)的反函数为y=f-1(x).若函数y=f(-x)的反函数是y=f-1(-x),则y=f(-x)是( )
| A. | 是奇函数,不是偶函数 | B. | 是偶函数,不是奇函数 | ||
| C. | 既是奇函数数,又是偶函数 | D. | 既不是奇函数,也不是偶函数 |
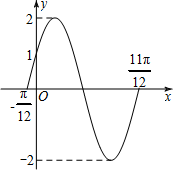 若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.
若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分图象如图所示.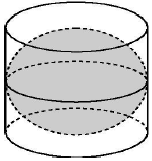 如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.
如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.