题目内容
7．
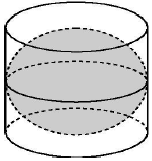如图是古希腊数学家阿基米德的墓碑文，墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等．相传这个图形表达了阿基米德最引以自豪的发现．我们来重温这个伟大发现．经计算球的体积等于圆柱体积的$\frac{2}{3}$倍．
分析 根据两图形的关系可得圆柱的底面半径与球的半径相等，设半径为r，计算出两几何体的体积，求出比值即可．
解答 解：∵圆柱内切一个球，∴圆柱的底面半径与球的半径相等，不妨设为r，
则圆柱的高为2r，
∴V圆柱=πr2•2r=2πr3，V球=$\frac{4}{3}π{r}^{3}$．
∴球与圆柱的体积之比为2：3，即球的体积等于圆柱体积的$\frac{2}{3}$倍．
故答案为$\frac{2}{3}$．
点评 本题考查了旋转体的结构特征，体积计算，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（c，0），圆M：（x-a）2+y2=c2，双曲线以椭圆C的焦点为顶点，顶点为焦点，若双曲线的两条渐近线都与圆M相切，则椭圆C的离心率为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{1}{2}$ |