题目内容
Rt△ABC中,AC=BC=
,CD⊥AB,沿CD将△ABC折成60°的二面角A-CD-B,则折叠后点A到平面BCD的距离是( )
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:由二面角的定义,即可得到∠ADB即为二面角A-CD-B的平面角,且为60°,由直角三角形的勾股定理,即可得到AD=BD=1,进而得到三角形ABD为等边三角形,取BD的中点E,连接AE,运用线面垂直的性质和判定定理,证得AE⊥平面BCD,则有点A到平面BCD的距离为AE.求出AE即可.
解答:
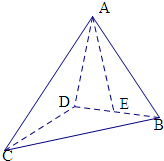 解:如图,AD⊥CD,BD⊥CD,
解:如图,AD⊥CD,BD⊥CD,
则∠ADB即为二面角A-CD-B的平面角,且为60°,
则在直角△ACD中,AC=
,CD=1,则AD=1,
在直角△ACD中,BC=
,CD=1,则BD=1,
则三角形ABD为等边三角形,
取BD的中点E,连接AE,
则AE⊥BD,
由于AD⊥CD,BD⊥CD,则CD⊥平面ABD,
由AE?平面ABD,则有CD⊥AE,
则有AE⊥平面BCD,则有点A到平面BCD的距离为AE.
而AE=
AD=
,
则所求距离为
,
故选C.
 解:如图,AD⊥CD,BD⊥CD,
解:如图,AD⊥CD,BD⊥CD,则∠ADB即为二面角A-CD-B的平面角,且为60°,
则在直角△ACD中,AC=
| 2 |
在直角△ACD中,BC=
| 2 |
则三角形ABD为等边三角形,
取BD的中点E,连接AE,
则AE⊥BD,
由于AD⊥CD,BD⊥CD,则CD⊥平面ABD,
由AE?平面ABD,则有CD⊥AE,
则有AE⊥平面BCD,则有点A到平面BCD的距离为AE.
而AE=
| ||
| 2 |
| ||
| 2 |
则所求距离为
| ||
| 2 |
故选C.
点评:本题考查线面垂直的性质和判定,考查二面角的求法,点到平面的距离的求法,考查运算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=