Question

已知某个四面体的棱长均为a，
（1）求该四面体外接球的体积；
（2）求该四面体内切球的体积．

Answer 1

考点：球的体积和表面积

专题：空间位置关系与距离

分析：（1）由正四面体的棱长为a，所以此四面体一定可以放在棱长为

2

2

a的正方体中，所以此四面体的外接球即为此正方体的外接球，由此能求出此四面体的外接球的半径，再代入面积公式、体积公式计算．
（2）设正四面体的内切球的半径为r，求得正四面体的每个面的面积S的值，正四面体的高h，用等体积法求出四面体内切球的半径，可得四面体内切球的体积．

解答： 解：（1）：∵正四面体的棱长为a，
∴此四面体一定可以放在正方体中，
∴我们可以在正方体中寻找此四面体．
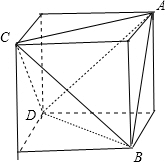
如图所示，四面体ABCD满足题意，BC=a，
∴正方体的棱长为

2

2

a，
∴此四面体的外接球即为此正方体的外接球，
∵外接球的直径=正方体的对角线长，
∴外接球的半径为R=

1

2

•

1 2 + 1 2 + 1 2

=

6

4

a，
所以，球的体积为

4

3

π•a³=

6

8

πa³．
（2）设正四面体的内切球的半径为r，由于正四面体的每个面的面积为S=

1

2

•a•a•sin60°=

3

4

a²，
正四面体的高为h=

a2-[ 2 3 • 3 2 a]2

=

6

3

a，
故正四面体的体积为V=

1

3

Sh=

2

12

a³．
再根据V=4[

1

3

sr]=4×[

1

3

•

3

4

a²•r]，可得

2

12

a³=4×[

1

3

•

3

4

a²•r]，求得r=

6

12

a，
故四面体内切球的体积V′=

4

3

π•r³=

6

216

π•a³．

点评：本题考查几何体的接体问题，考查了空间想象能力，其解答的关键是根据几何体的结构特征，求出接体几何元素的数据，代入面积、体积公式分别求解．