题目内容
已知x2+y2-6x+5=0,求x2+y2的最大值和最小值.
考点:点与圆的位置关系
专题:直线与圆
分析:x2+y2是圆上点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于C′,进而可知x2+y2的最大值和最小值分别为|OC′|和|OB|,答案可得.
解答:
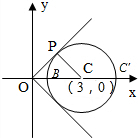 解:x2+y2-6x+5=0,化为(x-3)2+y2=4.圆的圆心坐标C(3,0)半径为2,
解:x2+y2-6x+5=0,化为(x-3)2+y2=4.圆的圆心坐标C(3,0)半径为2,
x2+y2的表示圆上的点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于C′,可知B到原点的距离最近,点C′到原点的距离最大,此时有OB=3-2=1,OC′=3+2=5,
则(x2+y2)max=|OC′|2=25,(x2+y2)min=|OB|2=1.
 解:x2+y2-6x+5=0,化为(x-3)2+y2=4.圆的圆心坐标C(3,0)半径为2,
解:x2+y2-6x+5=0,化为(x-3)2+y2=4.圆的圆心坐标C(3,0)半径为2,x2+y2的表示圆上的点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于C′,可知B到原点的距离最近,点C′到原点的距离最大,此时有OB=3-2=1,OC′=3+2=5,
则(x2+y2)max=|OC′|2=25,(x2+y2)min=|OB|2=1.
点评:本题主要考查了圆的方程的综合运用.考查了学生转化和化归的思想和数形结合的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了调查学生携带手机的情况,学校对高一、高二、高三三个年级的学生进行分层抽样调查,已知高一有学生1200人、高二有1100人;三个年级总共抽取了65人,其中高一抽取了20人,则高三年级的全部学生数为( )
| A、1500 | B、1200 |
| C、1600 | D、1300 |
函数y=sin(3x+
)的图象的一条对称轴是( )
| 3π |
| 4 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|
已知:△ABC中,a=
,b=3,∠B=60°,则∠A=( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示的曲线是y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,求这个函数的解析式.
如图所示的曲线是y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,求这个函数的解析式.