题目内容
已知在等差数列{an}中,a1=31,Sn是它的前n项和,S10=S22,求数列{an}的通项an和Sn.
考点:等差数列的前n项和,等差数列的性质
专题:等差数列与等比数列
分析:由S10=S22,得a11+a22=2a1+31d=0,从而an=-2n+33,Sn=na1+
d=32n-n2.
| n(n-1) |
| 2 |
解答:
解:因为S10=a1+a2+…+a10,
S22=a1+a2+…+a22,
又S10=S22,所以a11+a12+…+a22=0,
所以
=0,
即a11+a22=2a1+31d=0,
又a1=31,所以d=-2,…(6分)
所以an=-2n+33
Sn=na1+
d=31n-n(n-1)=32n-n2.…(12分)
S22=a1+a2+…+a22,
又S10=S22,所以a11+a12+…+a22=0,
所以
| 12(a11+a22) |
| 2 |
即a11+a22=2a1+31d=0,
又a1=31,所以d=-2,…(6分)
所以an=-2n+33
Sn=na1+
| n(n-1) |
| 2 |
点评:本题考查等差数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
已知α为第三象限角,且sinα(sinα+cosα)=cos2α,则tan2α的值为( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
函数y=
的图象大致是( )
| x3 |
| 3x-1 |
A、 |
B、 |
C、 |
D、 |
从{2,3,4}中随机选取一个数a,从{2,3,4}中随机选取一个数b,则b>a的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
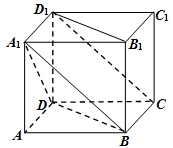 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60° 如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.
如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.