题目内容
判断下列函数的奇偶性,写出过程:
(1)f(x)=|x+1|
(2)f(x)=
,
(3)f(x)=x3
(4)f(x)=x2-2x
(5)f(x)=
.
(1)f(x)=|x+1|
(2)f(x)=
| x2 |
| 1+x2 |
(3)f(x)=x3
(4)f(x)=x2-2x
(5)f(x)=
| ||
|
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:判断函数的奇偶性主要掌握两点:(1)定义域所在的区间是否对称(2)f(-x)是否等于f(x)或
-f(x).
-f(x).
解答:
解:(1)f(x)=|x+1|的定义域为R 而f(-x)≠f(x)≠-f(x)
故为:非奇非偶函数
(2)f(x)=
的定义域为R,且f(-x)=f(x)
故为:偶函数
(3)f(x)=x3的定义域为R,且f(-x)=-f(x)
故为:奇函数
(4)f(x)=x2-2x的定义域为R,而f(-x)≠f(x)≠-f(x)
故为:非奇非偶函数
(5)f(x)=
的定义域为{x|-1≤x≤1}而f(-x)≠f(x)≠-f(x)
故为:非奇非偶函数
故答案为:①非奇非偶函数
②偶函数
③奇函数
④非奇非偶函数
⑤非奇非偶函数
故为:非奇非偶函数
(2)f(x)=
| x2 |
| 1+x2 |
故为:偶函数
(3)f(x)=x3的定义域为R,且f(-x)=-f(x)
故为:奇函数
(4)f(x)=x2-2x的定义域为R,而f(-x)≠f(x)≠-f(x)
故为:非奇非偶函数
(5)f(x)=
| ||
|
故为:非奇非偶函数
故答案为:①非奇非偶函数
②偶函数
③奇函数
④非奇非偶函数
⑤非奇非偶函数
点评:本题考查的知识点:判断函数奇偶性的标准及应用.

练习册系列答案
相关题目
从{2,3,4}中随机选取一个数a,从{2,3,4}中随机选取一个数b,则b>a的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}中,a1=2,an+1=an+cn(c是常数),且a1,a2,a3成公比不为1的等比数列,则a4=( )
| A、4 | B、8 | C、10 | D、14 |
方程x3-6x2+9x-10=0的实根个数是( )
| A、3 | B、2 | C、1 | D、0 |
函数y=
+
的定义域是( )
|
| 9-x |
A、(-
| ||
B、(-
| ||
C、[-
| ||
D、[-
|
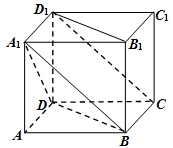 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60° 如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.
如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.