题目内容
已知f(x)=xlnx,g(x)=
,直线l:y=(k-3)x-k+2
(1)函数f(x)在x=e处的切线与直线l平行,求实数k的值
(2)若至少存在一个x0∈[1,e]使f(x0)<g(x0)成立,求实数a的取值范围
(3)设k∈Z,当x>1时f(x)的图象恒在直线l的上方,求k的最大值.
| ax2 |
| 2 |
(1)函数f(x)在x=e处的切线与直线l平行,求实数k的值
(2)若至少存在一个x0∈[1,e]使f(x0)<g(x0)成立,求实数a的取值范围
(3)设k∈Z,当x>1时f(x)的图象恒在直线l的上方,求k的最大值.
考点:导数在最大值、最小值问题中的应用,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求导,根据导数的几何意义得到关于k的方程解得即可.
(2)由于存在x0∈[1,e],使f(x0)<g(x0),则kx0>2lnx0⇒a>
,只需要k大于h(x)=
的最小值即可.
(3)分离参数,得到k<
,构造函数,求函数的最小值即可.
(2)由于存在x0∈[1,e],使f(x0)<g(x0),则kx0>2lnx0⇒a>
| 2lnx0 |
| x0 |
| 2lnx |
| x |
(3)分离参数,得到k<
| xlnx+3x-2 |
| x-1 |
解答:
解:(1)∵f′(x)=1+lnx,
∴f′(e)=1+lne=k-3
∴k=5,
(2)由于存在x0∈[1,e],使f(x0)<g(x0),
则
ax02>x0lnx0,
∴a>
设h(x)=
则h′(x)=
,
当x∈[1,e]时,h′(x)≥0(仅当x=e时取等号)
∴h(x)在[1,e]上单调递增,
∴h(x)min=h(1)=0,因此a>0.
(3)由题意xlnx>(k-3)x-k+2在x>1时恒成立
即k<
,
设F(x)=
,
∴F′(x)=
,
令m(x)=x-lnx-2,则m′(x)=1-
=
>0在x>1时恒成立
所以m(x)在(1,+∞)上单调递增,且m(3)=1-ln3<0,m(4)=2-ln4>0,
所以在(1,+∞)上存在唯一实数x0(x0∈(3,4))使m(x)=0
当1<x<x0时m(x)<0即F′(x)<0,
当x><x0时m(x)>0即F′(x)>0,
所以F(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增,
F(x)min=F(x0)=
=
=x0+2∈(5,6)
故k<x0+2又k∈Z,所以k的最大值为5
∴f′(e)=1+lne=k-3
∴k=5,
(2)由于存在x0∈[1,e],使f(x0)<g(x0),
则
| 1 |
| 2 |
∴a>
| 2lnx0 |
| x0 |
设h(x)=
| 2lnx |
| x |
则h′(x)=
| 2(1-lnx) |
| x2 |
当x∈[1,e]时,h′(x)≥0(仅当x=e时取等号)
∴h(x)在[1,e]上单调递增,
∴h(x)min=h(1)=0,因此a>0.
(3)由题意xlnx>(k-3)x-k+2在x>1时恒成立
即k<
| xlnx+3x-2 |
| x-1 |
设F(x)=
| xlnx+3x-2 |
| x-1 |
∴F′(x)=
| x-lnx-2 |
| (x-1)2 |
令m(x)=x-lnx-2,则m′(x)=1-
| 1 |
| x |
| x-1 |
| x |
所以m(x)在(1,+∞)上单调递增,且m(3)=1-ln3<0,m(4)=2-ln4>0,
所以在(1,+∞)上存在唯一实数x0(x0∈(3,4))使m(x)=0
当1<x<x0时m(x)<0即F′(x)<0,
当x><x0时m(x)>0即F′(x)>0,
所以F(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增,
F(x)min=F(x0)=
| x0lnx0+3x0-2 |
| x0-1 |
| x0(x0-2)+3x0-2 |
| x0-1 |
故k<x0+2又k∈Z,所以k的最大值为5
点评:本题考查导数在研究函数的单调性、函数恒成立的问题,考查等价转化的思想方法以及分析问题的能力,属于难题.

练习册系列答案
相关题目
若(a+bi)i=1+2i(其中i为虚数单位,a,b∈R),则a-b=( )
| A、-3 | B、3 | C、-1 | D、l |
若a>0>b,则下列不等式中成立的是( )
A、
| ||||
B、
| ||||
| C、|a|>|b| | ||||
| D、a2>b2 |
 已知三棱锥P-ABC,AB⊥BC,PA⊥PB,BC=6,AC=20,D为AC的中点,且△PCD是正三角形.
已知三棱锥P-ABC,AB⊥BC,PA⊥PB,BC=6,AC=20,D为AC的中点,且△PCD是正三角形.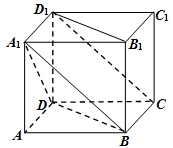 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°