题目内容
已知A，B，C，D，E为抛物线y=
x2上不同的五点，抛物线焦点为F，满足
+
+
+
+
=0，则|
|+|
|+|
|+|
|+|
|=（ ）
| 1 |
| 4 |
| FA |
| FB |
| FC |
| FD |
| FE |
| FA |
| FB |
| FC |
| FD |
| FE |
| A、5 | ||
| B、10 | ||
C、
| ||
D、
|
考点：抛物线的应用
专题：综合题,圆锥曲线的定义、性质与方程
分析：由题意可得，焦点F（0，1），准线为y=-1，由
+
+
+
+
=
，可得y1+y2+y3+y4+y5=5，根据抛物线的定义，可得结论．
| FA |
| FB |
| FC |
| FD |
| FE |
| 0 |
解答：
解：抛物线y=
x2的准线方程为y=-1，焦点坐标为（0，1）．
设A，B，C，D，E的纵坐标分别为y1，y2，y3，y4，y5，则
∵
+
+
+
+
=
，
∴y1-1+y2-1+y3-1+y4-1+y5-1=0，
∴y1+y2+y3+y4+y5=5，
根据抛物线的定义，可得|
|+|
|+|
|+|
|+|
|=y1+1+y2+1+y3+1+y4+1+y5+1=10，
故选B．
| 1 |
| 4 |
设A，B，C，D，E的纵坐标分别为y1，y2，y3，y4，y5，则
∵
| FA |
| FB |
| FC |
| FD |
| FE |
| 0 |
∴y1-1+y2-1+y3-1+y4-1+y5-1=0，
∴y1+y2+y3+y4+y5=5，
根据抛物线的定义，可得|
| FA |
| FB |
| FC |
| FD |
| FE |
故选B．
点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，得到y1+y2+y3+y4+y5=5是解题的关键．
练习册系列答案
相关题目
对?x∈R，函数f（x）=x2+bx+c的值恒非负，若b＞3，则
的最小值为（ ）
| 1+b+c |
| b-3 |
| A、3 | B、4 | C、5 | D、7 |
已知a，b∈R，且ab＞0，则下列不等式中不正确的是（ ）
A、
| ||||
B、2
| ||||
| C、|a+b|≥|a-b| | ||||
| D、|a+b|＜|a|+|b| |
已知F1，F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，若在右支上存在点A，使得点F2到直线AF1的距离为2a，则该双曲线的离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（1，
| ||
B、（1，
| ||
C、（
| ||
D、[
|
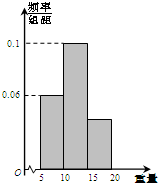如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为（ ）| A、10 | B、20 | C、30 | D、40 |
已知公差为2的等差数列{an}，若a4是a3与a7的等比中项，则a1=（ ）
| A、2 | B、3 | C、-2 | D、-3 |