题目内容
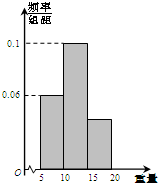如图是一容量为100的样本的重量的频率分布直方图，样本重量均在[5，20]内，其分组为[5，10），[10，15），[15，20]，则样本重量落在[15，20]内的频数为（ ）| A、10 | B、20 | C、30 | D、40 |
考点：频率分布直方图
专题：图表型,概率与统计
分析：频率分布直方图中各个小矩形的面积和为1，故先求出其它组的小矩形的面积，用1减去这些小矩形面积的和，求出[15，20]内的面积，即得出这一组的频率，用频率与样本容量100相乘得到这一组的频数．
解答：
解：第一个小矩形的面积为0.06×5=0.3，第二个小矩形的面积为0.1×5=0.5，
故[15，20]对应的小矩形的面积为1-0.3-0.5=0.2
样本落在[15，20]内的频率为0.2，
样本落在[15，20]内的频数为0.2×100=20，
故选B．
故[15，20]对应的小矩形的面积为1-0.3-0.5=0.2
样本落在[15，20]内的频率为0.2，
样本落在[15，20]内的频数为0.2×100=20，
故选B．
点评：本题考查对频率分布直方图的认识与了解，属于用图表告诉已知条件的题，此类题在高考中多有出现．
练习册系列答案
相关题目
设a∈R，若对任意的n∈N*时，不等式(an-20)ln(
)≥0恒成立，则a的取值范围是（ ）
| n |
| a |
| A、（-∞，5] |
| B、[4，5] |
| C、（4，5） |
| D、[1，5] |
中心在原点，焦点在x轴上的双曲线C的离心率为2，直线l与双曲线C交于A、B两点，线段AB中点M在第一象限，并且在抛物线y2=2px（p＞0）上，且M到抛物线焦点的距离为p，则直线l的斜率为（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知A，B，C，D，E为抛物线y=
x2上不同的五点，抛物线焦点为F，满足
+
+
+
+
=0，则|
|+|
|+|
|+|
|+|
|=（ ）
| 1 |
| 4 |
| FA |
| FB |
| FC |
| FD |
| FE |
| FA |
| FB |
| FC |
| FD |
| FE |
| A、5 | ||
| B、10 | ||
C、
| ||
D、
|
已知圆C：
（θ为参数），与x轴交与A、B两点，则|AB|等于（ ）
|
| A、6 | B、4 | C、2 | D、0 |