题目内容
(1)若对一切实数x,不等式|x-3|-|x+2|>a恒成立,求实数a的取值范围;
(2)若不等式|x-3|-|x+2|>a有解,求实数a的取值范围;
(3)若方程|x-3|-|x+2|=a有解,求实数a的取值范围.
(2)若不等式|x-3|-|x+2|>a有解,求实数a的取值范围;
(3)若方程|x-3|-|x+2|=a有解,求实数a的取值范围.
考点:绝对值不等式的解法
专题:计算题,函数的性质及应用
分析:(1)令f(x)=|x-3|-|x+2|=
,易求f(x)∈[-5,5],|x-3|-|x+2|>a恒成立?a<f(x)min,从而可得实数a的取值范围;
(2)不等式|x-3|-|x+2|>a有解?a<f(x)max,而f(x)∈[-5,5],于是可知实数a的取值范围;
(3)利用函数f(x)=|x-3|-|x+2|的值域为[-5,5],从而可得答案.
|
(2)不等式|x-3|-|x+2|>a有解?a<f(x)max,而f(x)∈[-5,5],于是可知实数a的取值范围;
(3)利用函数f(x)=|x-3|-|x+2|的值域为[-5,5],从而可得答案.
解答:
解:(1)令f(x)=|x-3|-|x+2|=
,
∴f(x)∈[-5,5],
∴f(x)min=-5;
∵|x-3|-|x+2|>a恒成立,
∴a<f(x)min=-5,
即实数a的取值范围为(-∞,-5);
(2)由(1)知,f(x)∈[-5,5],
∴不等式|x-3|-|x+2|>a有解?a<f(x)max=5,
即实数a的取值范围为(-∞,5);
(3)∵函数f(x)=|x-3|-|x+2|的值域为[-5,5],要使方程|x-3|-|x+2|=a有解,
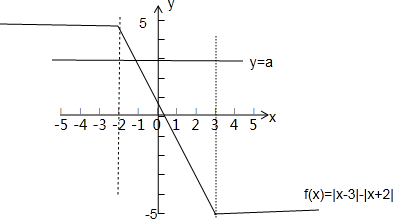
即函数f(x)=|x-3|-|x+2|与直线y=a有公共点,
∴-5≤a≤5,
∴实数a的取值范围为[-5,5].
|

∴f(x)∈[-5,5],
∴f(x)min=-5;
∵|x-3|-|x+2|>a恒成立,
∴a<f(x)min=-5,
即实数a的取值范围为(-∞,-5);
(2)由(1)知,f(x)∈[-5,5],
∴不等式|x-3|-|x+2|>a有解?a<f(x)max=5,
即实数a的取值范围为(-∞,5);
(3)∵函数f(x)=|x-3|-|x+2|的值域为[-5,5],要使方程|x-3|-|x+2|=a有解,
即函数f(x)=|x-3|-|x+2|与直线y=a有公共点,
∴-5≤a≤5,
∴实数a的取值范围为[-5,5].
点评:本题考查绝对值不等式的解法,考查等价转化思想与综合运算能力,考查作图与识图能力,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
已知A,B,C,D,E为抛物线y=
x2上不同的五点,抛物线焦点为F,满足
+
+
+
+
=0,则|
|+|
|+|
|+|
|+|
|=( )
| 1 |
| 4 |
| FA |
| FB |
| FC |
| FD |
| FE |
| FA |
| FB |
| FC |
| FD |
| FE |
| A、5 | ||
| B、10 | ||
C、
| ||
D、
|
已知点P(a,b)关于直线l的对称点为P′(b+1,a-1),则圆C:x2+y2-6x-2y=0关于直线L对称的圆C′的方程为( )
| A、(x-2)2+(y-2)2=10 |
| B、(x-2)2-(y-2)2=10 |
| C、(x-2)2+(y+2)2=10 |
| D、(x+2)2+(y-2)2=10 |