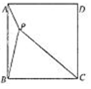
题目内容
5．若方程x2+（m+2）x+m+5=0只有负根，则m的取值范围是（ ）| A． | m≥4 | B． | -5＜m≤-4 | C． | -5≤m≤-4 | D． | -5＜m＜-2 |
分析 若方程x2+（m+2）x+m+5=0只有负根，则$\left\{\begin{array}{l}△=（m+2）^{2}-4（m+5）≥0\\-（m+2）＜0\\ m+5＞0\end{array}\right.$，解得m的取值范围．
解答 解：若方程x2+（m+2）x+m+5=0只有负根，
则$\left\{\begin{array}{l}△=（m+2）^{2}-4（m+5）≥0\\-（m+2）＜0\\ m+5＞0\end{array}\right.$，
解得：m≥4，
故选：A．
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
16．函数f（x）=3sin2x+2sinxcosx+cos2x-2的单调递减区间是（ ）
| A． | $[kπ+\frac{3π}{8}，kπ+\frac{7π}{8}]，k∈Z$ | B． | $[2kπ+\frac{3π}{8}，2kπ+\frac{7π}{8}]，k∈Z$ | ||
| C． | $[2kπ-\frac{π}{8}，2kπ+\frac{3π}{8}]，k∈Z$ | D． | $[kπ-\frac{π}{8}，kπ+\frac{3π}{8}]，k∈Z$ |
13．
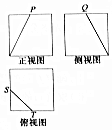一个几何体的三视图是如图所示的边长为2的正方形，其中P，Q，S，T为各边的中点，则此几何体的表面积是（ ）
一个几何体的三视图是如图所示的边长为2的正方形，其中P，Q，S，T为各边的中点，则此几何体的表面积是（ ）| A． | 21 | B． | $\frac{43}{2}$ | C． | $\frac{45}{2}$ | D． | 23 |