题目内容

16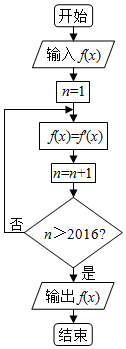．阅读如图所示的程序框图，其中f′（x）是f（x）的导数．已知输入f（x）为sinx，运行相应的程序，输出的结果是（　　）
A．sinxB．-sinxC．cosxD．-cosx

分析 按照程序框图的流程，写出前几次循环的结果，找到规律：函数解析式以4为一个周期，求出n=2016时输出经过的周期，得到输出的值．

解答 解：运行相应的程序，可得：
经过第一次循环得到cosx，n=2
经过第二次循环得到-sinx，n=3
经过第三次循环得到-cosx，n=4
经过第四次循环得到sinx，n=5
经过第五次循环得到cosx，n=6
…
观察规律可知，函数取值周期为4，当n=2016时，满足判断框中的条件执行输出，
∵2016÷4=504…0，
∴输出的结果是sinx．
故选：A．

点评 本题主要考查了循环结构的程序框图，解决程序框图中的循环结构时，常采用按照流程写出前几次循环的结果，找规律，属于基础题．

练习册系列答案
相关题目
17．已知$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-2，4），$\overrightarrow{c}$=（-1，-2）．
（1）求$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$任意两个向量夹角的余弦值；
（2）求$\overrightarrow{a}•\overrightarrow{b}$，（$\overrightarrow{a}-\overrightarrow{b}$）•（$\overrightarrow{a}+\overrightarrow{b}$），$\overrightarrow{a}•（\overrightarrow{b}+\overrightarrow{c}）$，（$\overrightarrow{a}+\overrightarrow{b}$）2的值．
7．当a为任意实数时，直线（a-1）x-y-a-1=0恒过定点C，则以C为圆心，半径为$\sqrt{5}$的圆的方程为（　　）
A．x2+y2-2x+4y=0B．x2+y2+2x+4y=0C．x2+y2+2x-4y=0D．x2+y2-2x-4y=0
4．下列函数中，既是偶函数又在（0，+∞）单调递增的函数是（　　）
A．y=x3B．y=|x|+1C．y=-x2+1D．y=2x
11．求点P（1，2，-2）和Q（-1，0，-1）间的距离3．
1．已知圆C：x2+y2=1，点P（x0，y0）在直线l：3x+2y-4=0上，若在圆C上总存在两个不同的点A、B，使$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OP}$，则x0的取值范围是 （　　）
A．（0，$\frac{24}{13}$）B．（-$\frac{24}{13}$，0）C．（0，$\frac{13}{24}$）D．（0，$\frac{13}{12}$）
8．设数列{an}的各项为正数，且a1，22，a2，24，…，an，22n，…成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）记Sn为等比数列{an}的前n项和，若Sk≥30（2k+1），求正整数k的最小值．
5．已知tanθ=2，则$\frac{1-sin2θ}{1+sin2θ}$=$\frac{1}{9}$．
6．设$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（m，1），如果向量$\overrightarrow{a}$+$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$平行，则$\overrightarrow{a}$•$\overrightarrow{b}$等于（　　）
A．-$\frac{5}{2}$B．-2C．-1D．0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网