题目内容
1.已知圆C:x2+y2=1,点P(x0,y0)在直线l:3x+2y-4=0上,若在圆C上总存在两个不同的点A、B,使$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OP}$,则x0的取值范围是 ( )| A. | (0,$\frac{24}{13}$) | B. | (-$\frac{24}{13}$,0) | C. | (0,$\frac{13}{24}$) | D. | (0,$\frac{13}{12}$) |
分析 根据条件可画出图形,根据图形便可看出OP的中点在圆内,从而可得到$\frac{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}{2}<1$,这样联立3x0+2y0-4=0即可得出x0的取值范围.
解答  解:如图,
解:如图,
∵$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OP}$;
∴OP与AB互相垂直平分;
∴圆心到直线AB的距离$\frac{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}{2}<1$;
∴${{x}_{0}}^{2}+{{y}_{0}}^{2}<4$①;
又3x0+2y0-4=0;
∴${y}_{0}=2-\frac{3}{2}{x}_{0}$,带入①得:
${{x}_{0}}^{2}+(2-\frac{3}{2}{x}_{0})^{2}<4$;
解得$0<{x}_{0}<\frac{24}{13}$;
∴x0的取值范围是$(0,\frac{24}{13})$.
故选:A.
点评 考查向量加法的平行四边形法则,圆心和弦中点的连线垂直于弦,以及两点间的距离公式,一元二次不等式的解法.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
12.下列函数中在定义域内既是奇函数又是增函数的为( )
| A. | y=2x+1 | B. | y=x2 | C. | y=$\frac{1}{x}$ | D. | y=x|x| |
9.已知a•b<|a•b|,则有( )
| A. | a•b<0 | B. | a<b<0 | C. | a>0,b<0 | D. | a<0<b |
16.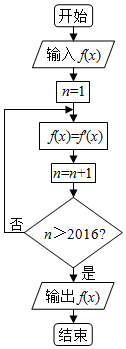 阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
 阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |