题目内容
8.设数列{an}的各项为正数,且a1,22,a2,24,…,an,22n,…成等比数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记Sn为等比数列{an}的前n项和,若Sk≥30(2k+1),求正整数k的最小值.
分析 (Ⅰ)推导出数列{an}是首项为2,公比为4的等比数列,由此能求出数列{an}的通项公式.
(Ⅱ)先求出等比数列{an}的前n项和Sn=$\frac{2}{3}({4}^{n}-1)$,从而得到$\frac{2}{3}({4}^{k}-1)$≥30(2k+1),由此能求出正整数k的最小值.
解答 解:(Ⅰ)∵列{an}的各项为正数,且a1,22,a2,24,…,an,22n,…成等比数列,
∴${{a}_{2}}^{2}={2}^{2}•{2}^{4}={2}^{6}$,即a2=8,
∴$\frac{{2}^{2}}{{a}_{1}}=\frac{8}{{2}^{2}}$,解得a1=2,
∴数列{an}是首项为a1=2,公比为q=$\frac{{a}_{2}}{{a}_{1}}$=4的等比数列,
∴${a}_{n}=2×{4}^{n-1}$.
(Ⅱ)∵数列{an}是首项为2,公比为4的等比数列,
∴等比数列{an}的前n项和Sn=$\frac{2(1-{4}^{n})}{1-4}$=$\frac{2}{3}({4}^{n}-1)$,
∵Sk≥30(2k+1),∴$\frac{2}{3}({4}^{k}-1)$≥30(2k+1),
即2×(2k)2-90×2k-92≥0,
解得2k≥46或2k≤-1(舍),
∴正整数k的最小值为6.
点评 本题考查数列的通项公式的求法,考查满足条件的正整数的最小值的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
16.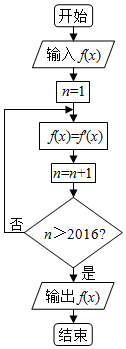 阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
 阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
3.执行如图所示的程序框图(算法流程图),输出的结果是( )


| A. | 9 | B. | 121 | C. | 130 | D. | 17021 |
20.已知A,B,C是复平面内的三个不同点,点A,B对应的复数分别是-2+3i,-i,若$\overrightarrow{AC}$=$\overrightarrow{CB}$,则点C表示的复数是( )
| A. | -2+2i | B. | -2+4i | C. | -1+i | D. | -1+2i |
17.执行如图所示程序框图,则输出的n为( )


| A. | 4 | B. | 6 | C. | 7 | D. | 8 |